قفل‌شدگی حجمی (Volumetric Locking) چیست؟
قفل‌شدگی حجمی (Volumetric Locking) در روش المان محدود (FEM) هنگامی رخ می‌دهد که رفتار ماده تقریباً تراکم ناپذیر (مثل لاستیک = rubber like) باشد و همزمان از انتگرال‌گیری کامل (full integration) استفاده شده باشد. قفل‌شدگی حجمی (Volumetric Locking) موجب می‌شود که سفتی (stiffness) المان بیش از مقدار اصلی تخمین زده شود (Overestimate). در هنگامی که رفتار ماده تقریباً تراکم ناپذیر (nearly incompressible) است، توصیه می‌شود که از المان هایبرید (hybrid element) استفاده شود.
Volumetric locking represents one of the most challenging numerical artifacts in finite element analysis, particularly when modeling materials with nearly incompressible behavior. This phenomenon significantly impacts solution accuracy, leading to artificially stiff responses and unreliable stress predictions.
اگر رفتار ماده تراکم ناپذیر (incompressible) باشد، مسئله را تنها با درجات آزادی (DOF) جابجایی نمی‌توان تحلیل کرد زیرا فشار هیدرواستاتیک در المان‌ها قابل محاسبه نیست. به عبارت دیگر اضافه شدن فشار هیدرواستاتیک تعییری در میدان جابجایی (Displacment Field) ایجاد نمی‌کند. برای تحلیل این مسائل لازم است از ضریب لاگرانژ (Lagrange multiplier) یا درجه آزادی (DOF) فشار هیدرواستاتیک استفاده شود.
در مسائلی که رفتار ماده تقریباً تراکم ناپذیر (nearly incompressible) است، حساسیت محاسبات نسبت به خطاها به شدت بالا می‌رود، از این رو امکان وقوع قفل‌شدگی حجمی (Volumetric Locking) وجود دارد. در واقع قفل‌شدگی حجمی (Volumetric Locking) ناشی از محدودیت محاسبات عددی است.
Volumetric locking represents a mathematical limitation of standard finite element formulations that struggle to satisfy the incompressibility constraint without overconstraining the solution space.
قفل‌شدگی حجمی (Volumetric Locking) در چه صورت رخ می‌دهد؟
رفتار ماده تقریباً تراکم ناپذیر (nearly incompressible)
رفتار تقریباً تراکم ناپذیر مواد و رفتار پلاستیک فلزات (فلزات در ناحیه پلاستیک حجم ثابت دارند / isochoric ) می‌تواند موجب قفل‌شدگی حجمی (Volumetric Locking) شود.
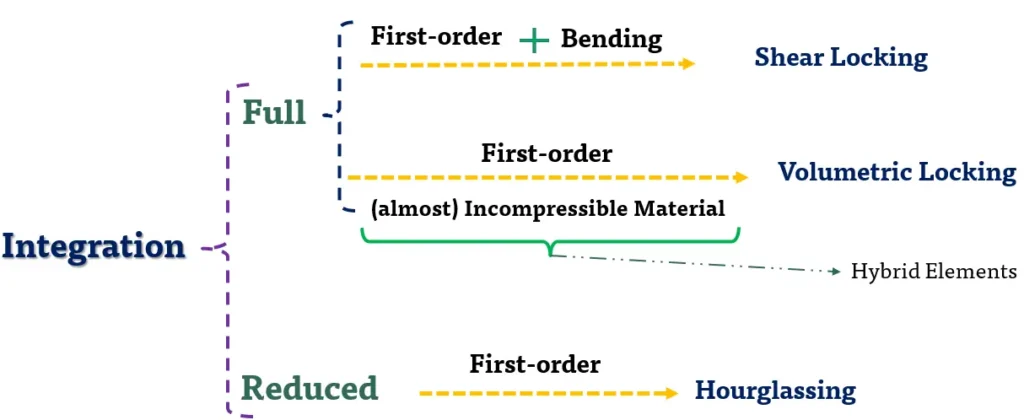
انتگرال‌گیری کامل (Full Integration) در المان‌های مرتبه اول (First-order)
روش‌های جلوگیری از قفل‌شدگی حجمی (Volumetric Locking)
استفاده از مش ریز (Fine Mesh)
استفاده از انتگرال‌گیری کاهش‌یافته (Reduced Integration)
استفاده از انتگرال‌گیری کاهش‌یافته انتخابی (Selective Reduced Integration)
استفاده از روش B-bar و F-bar
استفاده از Mixed Formulation یا Hybrid Formulation
انتگرال‌گیری عددی (Numerical Integration) در روش المان محدود (FEM)
در روش المان محدود (FEM) انتگرال‌گیری‌ها (integrations) با روش‌های عددی (numerical methods) به خصوص روش گوس (gauss quadrature) محاسبه می‌شوند. تعداد نقاط انتگرال‌گیری با توجه به مرتبه المان (element order) و کامل (full) یا کاهش‌یافته (reduced) بودن انتگرال‌گیری مشخص می‌شود. برای مثال در نرم افزار آباکوس (Abaqus) تعداد نقاط انتگرال‌گیری برای المان چهارضلعی (quadrilateral) مطابق تصویر زیر است.
بنابراین در نرم افزار آباکوس (Abaqus) اگر المان مرتبه اول (first-order/linear) باشد، در حالت انتگرال‌گیری کامل (full integration) در هر راستا دو نقطه و در حالت انتگرال‌گیری کاهش یافته (reduced integration) یک نقطه در هر راستا در نظر گرفته می‌شود در حالی‌که اگر المان مرتبه دوم (secend-order/quadratic) باشد، در حالت انتگرال‌گیری کامل (full integration) در هر راستا سه نقطه و در حالت انتگرال‌گیری کاهش یافته (reduced integration) دو نقطه در هر راستا در لحاظ می‌شود.
استفاده از المان مرتبه اول (first-order/linear) در تحلیل‌های المان محدود (FEA) موجب افزایش چشمگیر سرعت محاسبات یا همان CPU time می‌شود. استفاده از انتگرال‌گیری کاهش یافته (reduced integration) در محاسبات نیز باعث کاهش حجم محاسبات می‌شود. بنابراین معمولا اولویت استفاده از المان مرتبه اول و انتگرال‌گیری کاهش یافته است اما باید نکات لازم را در نظر گرفت تا دقت محاسبات تحت تاثیر قرار نگیرد.
نویسنده:
مهندس میلاد وحیدیان
دانشجوی دکترای مهندسی مکانیک دانشگاه تهران
(برای مطالعه بیشتر روی نام یا تصویر ایشان کلیک کنید)