یکی از مراحل مهم در تحلیل المان محدود (FEA)، انتخاب المان (Element) مناسب است. هر یک از تحلیلهای المان محدود (FEA) بار محاسباتی زیادی دارند. علاوه بر این برای بررسی استقلال نتایج تحلیل از نوع المان و اندازه آن (mesh independency) باید چند بار مسئله با المان و اندازه مش متفاوت تحلیل شود. از این رو تلاش میشود که از المان مرتبه اول (first order) یا المان خطی (linear) به حای المانهای مرتبه بالا و انتگرالگیری عددی کاهش یافته (reduced integration) به جای انتگرالگیری کامل (full integration) استفاده میشود.
ویژگیهای المان (Element Aspect) یا نوع المان (Element Type)
برای انتخاب درست المان باید به موارد زیادی توجه کنیم تا هم دقت محاسبات مناسب باشد و هم تا حد امکان بار محاسباتی کمتر باشد. دستهبندیهای مطرح شده در اینجا بر اساس مستندات آباکوس (Abaqus Documentation) است و ممکن است در برخی منابع کمی متفاوت باشد. برای مثال بعضی منابع نوع المان را بر اساس بعد المان (یکبعدی – دوبعدی و سهبعدی) طبقهبندی میکنند.
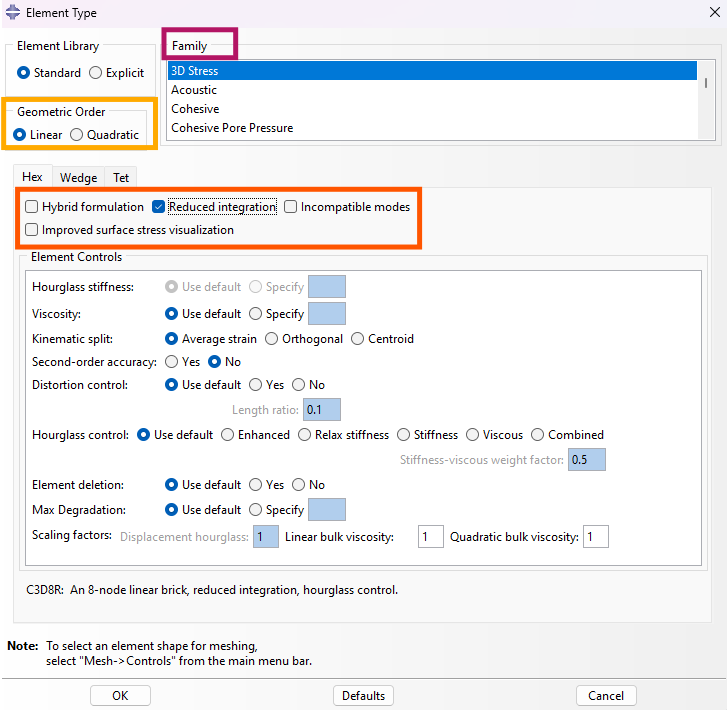
خانواده المان (Element Family)
خانواده المان (Element Family) شامل بعد المان (یک بعدی – دوبعدی – سهبعدی) و نوع سازه مسئله (خرپا – تیر – غشاء – تنش صفحهای – کرنش صفحهای – تقارن محوری – پوسته – سالید) است. در اصل تمامی مسائل سهبعدی هستند و باید با المانهای سهبعدی و معادلات حاکم در سهبعد تحلیل شوند.
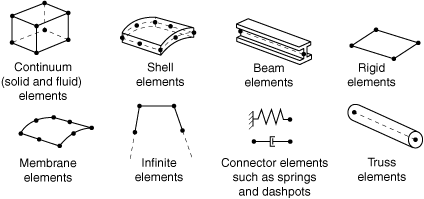
در برخی موارد هندسه مسئله، بارگذاریها و شرایط مرزی به نحوی است که میتوان مسئله را کمی سادهتر تحلیل کرد و به جای تحلیل مسئله در سهبعد، تحلیل دو بعدی (تنش صفحهای – کرنش صفحهای – تقارن محوری) یا حتی تحلیل یک بعدی (خرپا – تیر) انجام شود. اگر چه با این کار فرضیات ساده کنندهای اعمال شده است ولی نتایج با حالت سهبعدی تطابق بسیار خوبی دارند.
مرتبه درونیابی المان (Element Interpolation Order) یا مرتبه هندسی المان (Element Geometric Order)
برای گسستهسازی (discretization) مسئله یعنی تبدیل متغیرهای پوسته مثل جابجایی ( u(x,y,z) ) به متغیرها گرهای (nodal variables) از روابط درونیابی (interpolation) خطی یا مرتبه اول، مرتبه دوم یا quadratic، مرتبه سوم یا cubic استفاده میشود. هرچه مرتبه درونیابی یا مرتبه المان بالاتر باید دقت تحلیل و بار محاسباتی بیشتر است.
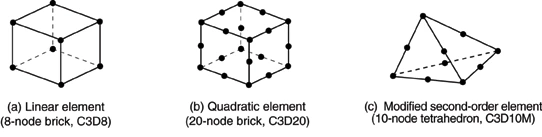
در مسائلی که تمرکز تنش (stress concentration) وجود دارد توصیه میشود از المانهای مرتبه بالا (high-order) مثل المان مرتبه دو (second-order/quadratic) یا المان مرتبه سوم (cubic/second-order) استفاده شود
روابط المان (Element Formulation)
معادلات ریاضی و تئوریهای استفاده در المان را روابط المان (Element Formulation) میگویند. برای مثال المان پوسته (shell) از نوع general purpose – thin shell – thick shell وجود دارد.
انتگرالگیری المان (Element Integration)
برای محاسبه انتگرالها از روشهای عددی مثل Simpson و Guess استفاده میشود. در این روشها انتگرال با سیگما زیر جایگزین میشوند که در آن نقاظ انتگرالگیری با r,s,t و توابع وزنی هر نقطه انتگرالگیری با wi, wj, wk مشخص شده است.
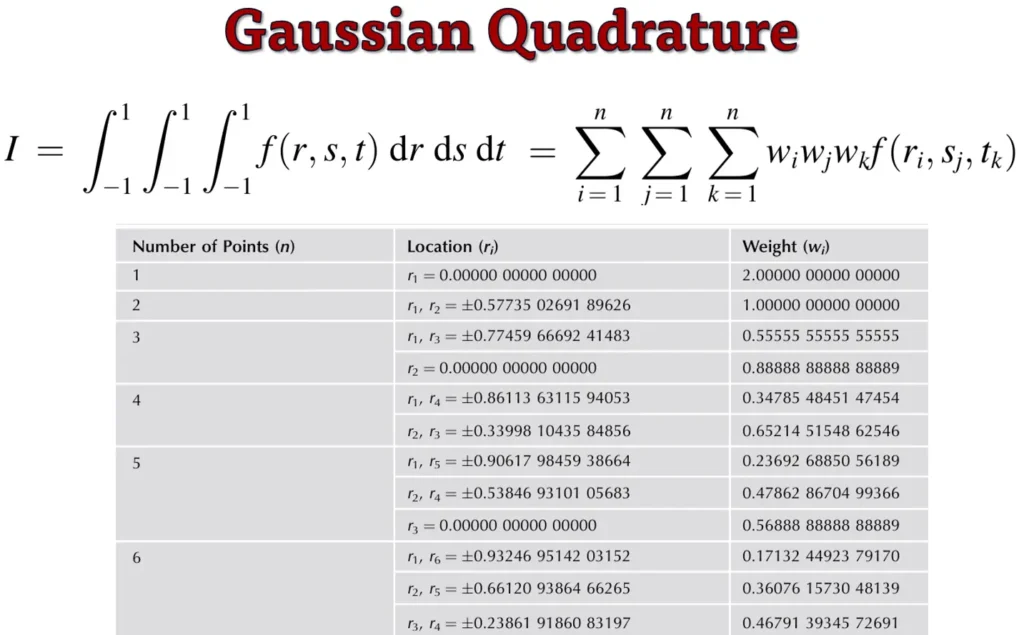
برای کاهش بار محاسبات انتگرالگیریها میتوان از به جای استفاده از تعداد نقاط لازم یعنی اننگرالگیری کامل (full integration) از نقاط انتگرالگیری کمتری استفاده کرد که به آن انتگرال کاهشیافته (reduced integration) گفته میشود.

اگر چه استفاده از المان مرتبه اول و انتگرالگیری کاهش یافته بار محاسباتی را کاهش میدهد، اما ممکن است درگیر پدیدههایی مثل ساعتنشی (hourglass) و … شویم.
چند توصیه برای انتخاب المان مناسب (Suitable Element)
1- با استفاده از verify mesh شکل المانها را بررسی کنید که زوایا و نسبت اضلاع المان مناسب باشید (well shaped)
2- تا حد امکان در مسائل دوبعدی از المانهای چهار ضلعی (quadrilateral) و در مسائل سهبعدی از المانهای شش وجهی (hexahedral) استفاده شود.
3- اگر از المانهای مثلثی (triangular) یا المانهای چهار وجهی (tetrahedral) استفاده کردید، از المان مرتبه بالا مثل quadratic استفاده شود.
4- در تحلیلهای خطی و غیرخطی هموار (smooth) المان مرتبه دوم (second-order / quadratic) و انتگرالگیری کاهشیافته (reduced-integration) انتخاب خوبی است.
5- در نزدیکی نقاط تمرکز تنش (Stress Concentration) حتما از المانهای مرتبه دوم (second-order / quadratic) و انتگرالگیری کامل (full-integration) استفاده شود.
6- در تحلیلهایی که رفتار ماده تراکم ناپذیر (incompressible) یا تقیریبا تراکم ناپذیر (nearly incompressible) است از المانهای هایبرید (Hybrid elements) استفاده شود.
7- در مسائلی که خمش غالب (bending-dominated) است، المان Incompatible mode دقت تحلیل را به طور چشمگیری افزایش میدهد و از قفلشوندگی برشی (shear locking) جلوگیری میکند.
8- در صورتی که از المان مرتبه اول (first-order / linear) و انتگرالگیری کامل (full integration) استفاده کردید، از مش زیر استفاده کنید تا درگیر پدیدههای قفلشوندگی برشی (shear locking) و قفلشوندگی حجمی (volumetric locking) نشوید.
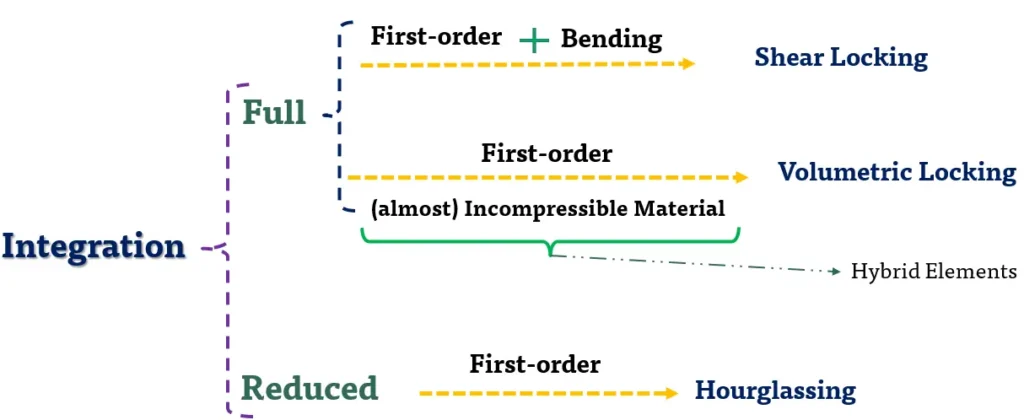
9- در صورتی که از المان مرتبه اول (first-order / linear) و انتگرالگیری کاهشیافته (reduced integration) استفاده کردید، مراقب پدیده ساعتشنی (hourglass) باشید.
نویسنده:
مهندس میلاد وحیدیان
دانشجوی دکترای مهندسی مکانیک دانشگاه تهران
(برای مطالعه بیشتر روی نام یا تصویر ایشان کلیک کنید)


