قفلشدگی برشی (Shear Locking) در چه صورت رخ میدهد؟
قفلشدگی برشی (Shear Locking) نوعی خطای عددی (numerical error) در تحلیل المان محدود (FEA) است که بارگذاری خمشی (bending) غالب باشد و همزمان از المانهای مرتبه اول (first-order) و انتگرالگیری کامل (full integration) استفاده شده باشد. قفلشوندگی برشی (Shear Locking) موجب ایجاد کرنش برشی مجازی (artificial shear strain) در المان و در نتیجه سفتی (stiffness) المان بیش از مقدار اصلی تخمین زده میشود (Overestimate).
Shear locking is a numerical error that occurs when linear (first-order) elements cannot properly represent the kinematics of bending deformation. It manifests primarily in fully integrated first-order elements that are subjected to bending loads
چرا قفلشدگی برشی (Shear Locking) رخ میدهد؟
قفلشدگی (Shear Locking) در روش المان محدود (FEM) به دلیل عدم توانایی المانهای مرتبه اول (first-order) در به تصویر کشیدن خطوط منحنی شکل است.
The essence of shear locking lies in the element’s inability to correctly capture the kinematics of deformation during bending.
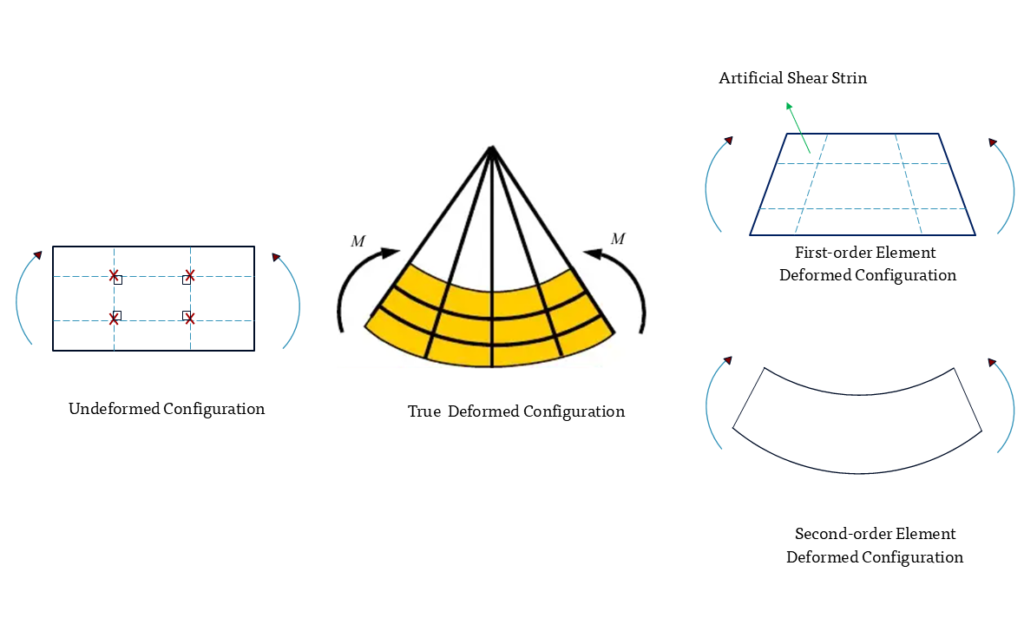
این تغییر شکل ناسازگار با فیزیک مسئله باعث تولید کرنشهای بررشی غیر واقعی (مجازی) و در نتیجه موجب افزایش سفتی (stiffness) المان میشود.
روشهای جلوگیری از قفلشدگی برشی (Shear Locking)
استقاده از مش ریز (Fine Mesh)
یکی از سادهترین راههای مقابله با قفلشدگی برشی (Shear Locking)، استفاده از مشبندی ریز و کوچک است که بار محاسباتی مسئله را به شدت بالا میبرد.
استفاده از المان مناسب
استفاده از المان مرتبه دوم (second-order / quadratic) یا المان با فرمولاسیون یا تکنیکهای ضدقفل (anti-locking) میتواند راهگشا باشد.
استفاده از انتگرالگیری کاهشیافته (reduced integration)
هرچند استفاده از انتگرالگیری کاهشیافته (reduced integration) موجب پیشگیری از قفلشدگی برشی (Shear Locking) میشود، اما باید دقت شود که استفاده از انتگرالگیری کاهشیافته (reduced integration) و المان مرتبه میتواند موجب پدیده ساعتشنی (hourglassing) شود.
استفاده از المانهای Incompatible mode در Abaqus
انتگرالگیری عددی (Numerical Integration) در روش المان محدود (FEM)
در روش المان محدود (FEM) انتگرالگیریها (integrations) با روشهای عددی (numerical methods) به خصوص روش گوس (gauss quadrature) محاسبه میشوند. تعداد نقاط انتگرالگیری با توجه به مرتبه المان (element order) و کامل (full) یا کاهشیافته (reduced) بودن انتگرالگیری مشخص میشود. برای مثال در نرم افزار آباکوس (Abaqus) تعداد نقاط انتگرالگیری برای المان چهارضلعی (quadrilateral) مطابق تصویر زیر است.

بنابراین در نرم افزار آباکوس (Abaqus) اگر المان مرتبه اول (first-order/linear) باشد، در حالت انتگرالگیری کامل (full integration) در هر راستا دو نقطه و در حالت انتگرالگیری کاهش یافته (reduced integration) یک نقطه در هر راستا در نظر گرفته میشود در حالیکه اگر المان مرتبه دوم (secend-order/quadratic) باشد، در حالت انتگرالگیری کامل (full integration) در هر راستا سه نقطه و در حالت انتگرالگیری کاهش یافته (reduced integration) دو نقطه در هر راستا در لحاظ میشود.
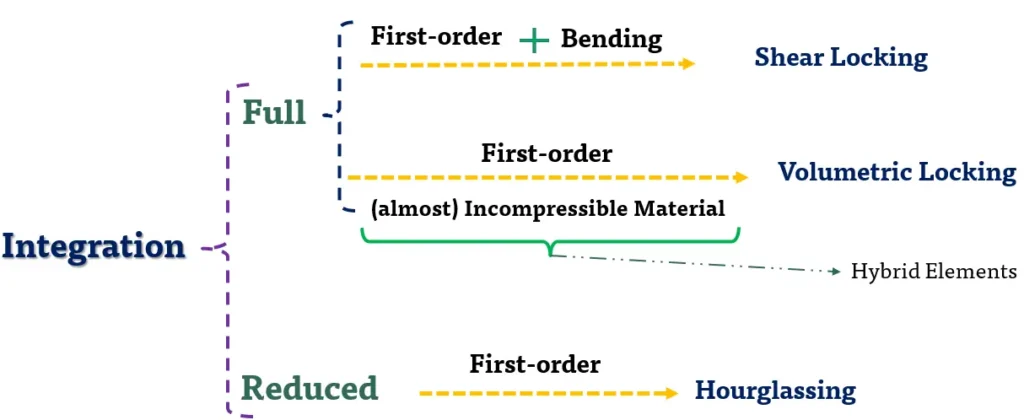
استفاده از المان مرتبه اول (first-order/linear) در تحلیلهای المان محدود (FEA) موجب افزایش چشمگیر سرعت محاسبات یا همان CPU time میشود. استفاده از انتگرالگیری کاهش یافته (reduced integration) در محاسبات نیز باعث کاهش حجم محاسبات میشود. بنابراین معمولا اولویت استفاده از المان مرتبه اول و انتگرالگیری کاهش یافته است اما باید نکات لازم را در نظر گرفت تا دقت محاسبات تحت تاثیر قرار نگیرد.
Shear and Volumetric Locking according to Abaqus Documentation
Fully integrated elements in Abaqus/Standard and Abaqus/Explicit do not hourglass but may suffer from “locking” behavior: both shear and volumetric locking. Shear locking occurs in first-order, fully integrated elements (CPS4, CPE4, C3D8, etc.) that are subjected to bending. The numerical formulation of the elements gives rise to shear strains that do not really exist—the so-called parasitic shear. Therefore, these elements are too stiff in bending, in particular if the element length is of the same order of magnitude as or greater than the wall thickness. See Performance of continuum and shell elements for linear analysis of bending problems for further discussion of the bending behavior of solid elements.
Volumetric locking occurs in fully integrated elements when the material behavior is (almost) incompressible. Spurious pressure stresses develop at the integration points, causing an element to behave too stiffly for deformations that should cause no volume changes. If materials are almost incompressible (elastic-plastic materials for which the plastic strains are incompressible), second-order, fully integrated elements start to develop volumetric locking when the plastic strains are on the order of the elastic strains. However, the first-order, fully integrated quadrilaterals and hexahedra use selectively reduced integration (reduced integration on the volumetric terms). Therefore, these elements do not lock with almost incompressible materials. Reduced-integration, second-order elements develop volumetric locking for almost incompressible materials only after significant straining occurs. In this case, volumetric locking is often accompanied by a mode that looks like hourglassing. Frequently, this problem can be avoided by refining the mesh in regions of large plastic strain.
If volumetric locking is suspected, check the pressure stress at the integration points (printed output). If the pressure values show a checkerboard pattern, changing significantly from one integration point to the next, volumetric locking is occurring. Choosing a quilt-style contour plot in the Visualization module of Abaqus/CAE will show the effect.
: Summary
The formulation and order of integration used in a continuum element can have a significant effect on the accuracy and cost of the analysis.
First-order (linear) elements using full integration are prone to shear locking and normally should not be used.
First-order, reduced-integration elements are prone to hourglassing; sufficient mesh refinement minimizes this problem.
When using first-order, reduced-integration elements in a simulation where bending deformation will occur, use at least four elements through the thickness.
Hourglassing is rarely a problem in the second-order, reduced-integration elements in Abaqus/Standard. You should consider using these elements for most general applications when there is no contact.
The accuracy of the incompatible mode elements available in Abaqus/Standard is strongly influenced by the amount of element distortion.
The numerical accuracy of the results depends on the mesh that has been used. Ideally a mesh refinement study should be carried out to ensure that the mesh provides a unique solution to the problem. However, remember that using a converged mesh does not ensure that the results from the finite element simulation will match the actual behavior of the physical problem: that also depends on other approximations and idealizations in the model.
In general, refine the mesh mainly in regions where you want accurate results; a finer mesh is required to predict accurate stresses than is needed to calculate accurate displacements.
Advanced features such as submodeling are available in Abaqus to help you to obtain useful results for complex simulations.
نویسنده:
مهندس میلاد وحیدیان
دانشجوی دکترای مهندسی مکانیک دانشگاه تهران
(برای مطالعه بیشتر روی نام یا تصویر ایشان کلیک کنید)


