مقایسه حلگر ضمنی (Implicit) و حلگر صریح (Explicit)

حلگر ضمنی (Implicit) و حلگر صریح (Explicit)

حلگر ضمنی (Implicit) یا حلگر صریح (Explicit)؟ یکی از سوالات رایج کاربران نرم افزارهای المان محدود از جمله آباکوس (Abaqus) این است که حلگر (solver) مناسب برای تحلیل مسئله شان کدام است؟ یا به عبارتی دیگر باید از حلگر آباکوس استاندارد (Abqus/Standard) که حلگری ضمنی (Implicit) است استفاده کنند یا آباکوس اکسپلیسیت (Abaqus/Explicit) که حلگر صریح (Explicit) است؟

اغلب نرم افزارهای تحلیل المان محدود (FEA) از جمله نرم افزار آباکوس (Abaqus) حلگرهای (solvers) زیادی دارند اما پرکارد‌ترین این حلگر‌ها، حلگر ضمنی (Implicit) و حلگر صریح (Explicit) است که در نرم افزار آباکوس (Abaqus) به نام‌های آباکوس استاندارد (Abqus/Standard) و آباکوس اکسپلیسیت (Abaqus/Explicit) شناخته می‌شوند.

تمامی مسائل دنیای واقعی دینامیک (dynamics) هستند اگر تاثیر ایرنسی (inertia) در تحلیل مسئله کم یا ناچیز باشد می‌توان مسئله را به صورت استاتیکی تحلیل کرد. در مسائل استاتیک غیرخطی زمان عملا همان نموهای (increments) حل مسئله هستند.

به طور خلاصه تفاوت حلگر ضمنی (Implicit) و حلگر صریح (Explicit) در رویکردشان برای انتگرال گیری زمانی (time integration) مسئله است. این تفاوت روند انتگرال گیری زمانی (time integration)، محاسبات مسئله را به کلی تغییر می‌دهد به نحوی که حلگر صریح (Explicit) برای مسائل دینامیک سریع و گذارا (transiant) مثل برخود (impact) بهتر است و حلگر ضمنی (Implicit) برای سایر مسائل مناسب‌تر است.

تحلیل به کمک روش المان محدود (FEA)

معادلات حاکم (governing equations) بر اغلب مسائل مهندسی از نوع معادلات دیفرانسیل (differential equation) است. بنابراین مهندسین باید به دنبال یادگیری و استفاده از روش‌هایی قدرتمند برای حل معادلات دیفرانسیل معمولی (Ordinary Differential Equation=ODE) و معادلات دیفرانسیل با مشتقات جزئی (Partial Differential Equation=PDE) باشند. روش المان محدود (Finite Element Method=FEM) یکی از مشهورترین روش‌های عددی برای حل معادلات دیفرانسیل اعم از معادلات دیفرانسیل معمولی (ODE) خطی و غیرخطی و معادلات دیفرانسیل با مشتقات جزئی خطی و غیرخطی (PDE) است.

اساس روش المان محدود شامل مراحل زیر است:

1. گسسته‌سازی هندسه (Discretization)
2. در نظر گرفتن تابعی برای فرم کلی پاسخ در هر المان بر حسب مقادیر گره‌ای (Interpolation Function or Shape Function)
3. محاسبه ماتریس‌های مشخصه (ماتریس اینرسی خطی (جرم)، ماتریس اینرسی دورانی، ماتریس دمپینگ (میرائی) و ماتریس سفتی) برای هر المان (Element Characteristics Matrix)
4. مونتاژ المان‌ها برای ساخت ماتریس‌های مشخصه کل سازه (Assemblage)
5. اعمال شرایط مرزی به دستگاه معادلات ماتریسی (Apply Boundary Conditions)
6. اعمال شرایط اولیه در مسائل دینامیک (Apply Initial Conditions)
7. حل دستگاه معادلات جبری (در مسائل استاتیک) یا حل دستگاه معادلات دیفرانسیل معمولی (در مسائل دینامیک)

بنابراین در کلی‌ترین حالت، روش المان محدود (FEM) معادلات دیفرانسیل با مشتقات جزئی (PDE) را به معادلات دیفرانسیل با مشتقات معمولی (ODE) تبدیل می‌کند. فرم کلی معادلات گسسته شده (discretized) در مختصات مکانی/فضایی (spatial) را به صورت زیر است.

که در آن {a} متغییرهای گره‌ای (nodal variables) و t زمان است.

برای محاسبه متغییرهای گره‌ای (nodal variables) مغادله بالا، باید از معادلات انتگرال گیری زمانی (گسسته‌سازی مسئله در حوزه زمان) گرفته شود.

روش‌های انتگرال‌گیری عددی در حوزه زمان (Time Integration)

برای درک بهتر و ساده‌تر مفهوم انتگرال‌گیری زمانی به روش‌های ضمنی (Implicit) و صریح (Explicit) معادلات حاکم بر مسئله از مرتبه اول درنظر گرفته شده است. تصویر زیر به خوبی این مفاهیم را توصیف می‌کند.

روش‌ انتگرال‌گیری صریح (Explicit) یا حلگر صریح (Explicit)

در روش‌ انتگرال‌گیری صریح (Explicit)، مشتق دوم متغیر میدانی (به عنوان مثال شتاب) در زمان مطلوب تابعی صریح از همان متغیر میدانی در نمو زمانی (time increment) قبلی است. به رابطه زیر دقت کنید.

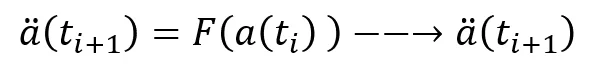
در روش‌ انتگرال‌گیری صریح (Explicit)، ماتریس اینرسی به صوت پارامتر Lumped در نظر گرفته می‌شود. بنابراین این ماتریس قطری خواهد بود و به سادگی معکوس (Inverse) ماتریس اینرسی را می‌توان محاسبه کرد. برای پایداری روش‌ انتگرال‌گیری صریح، نمو زمانی باید از stable time کوچکتر باشد. بنابراین این روش انتگرال‌گیری تحت شرایط خاصی پایدار است.

The explicit Method aims to solve acceleration and in most cases, the mass matrix is considered “lumped” and consequently mass matrix is a diagonal matrix. Explicit methods calculate the state of a system at a later time from the state of the system at the current time.

Once the accelerations are calculated at the nth step, the velocity at n+1/2 step and displacement at n+1 step are calculated accordingly. In these calculations, the scheme is not unconditionally stable and thus smaller time steps are required.

حداقل نمو زمانی (time increment) برای روش‌ انتگرال‌گیری صریح (Explicit) یا حلگر صریح (Explicit) از رابطه زیر محاسبه می‌شود.

روش‌ انتگرال‌گیری ضمنی (Implicit) یا حلگر ضمنی (Implicit)

در روش‌ انتگرال‌گیری ضمنی (Implicit)، متغیر میدانی (به عنوان مثال جابجایی) در زمان مطلوب تابعی ضمنی از همان متغیر میدانی در همان نمو زمانی (time increment) است. بنابراین در کلی‌ترین حالت پس از استفاده از الگوریتم‌های انتگرال‌گیری Implicit (مانند روش Newmark-beta) نیاز به یکی از روش‌های حل دسته معادلات جبری غیرخطی مانند روش نیوتن-رافسون (Newton-Raphson) است.

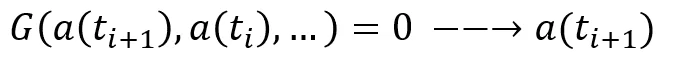
The implicit method involves the solution for the current step, which is based on the solution from the current step. These solutions are unconditionally stable and facilitate larger time steps. Despite this advantage, the implicit methods can be extremely time-consuming when solving dynamic and nonlinear problems.

موارد استفاده از حلگر Explicit و Abaqus/Explicit:

ابتدا توضیحات هلپ آباکوس (Abaqus documentation) در مورد حلگر Abaqus/Explicit را مرور کنیم:

Abaqus/Explicit: is a special-purpose analysis product that uses an explicit dynamic finite element formulation. It is suitable for modeling brief, transient dynamic events, such as impact and blast problems, and is also very efficient for highly nonlinear problems involving changing contact conditions, such as forming simulations. Abaqus/Explicit is ideal for analyses where high-speed, non-linear, transient response dominates the solution.

حلگر Explicit، حلگری مخصوص مسائل دینامیک گذارا است. برای مثال برای شبیه‌سازی مسائل برخورد، انفجار باید از این حلگر قدرتمند استفاده کنیم. علاوه بر این در مسائلی که شرایط مرزی تماس پیچیده (مثل تغییر شرایط تماس) است، مانند فرایندهای شکل‌دهی، این حلگر تنها گزینه مناسب خواهد بود زیرا حلگر Implicit دچار مشکل همگرایی خواهد شد.

موارد استفاده از حلگر Implicit و Abaqus/Standard:

ابتدا توضیحات هلپ آباکوس (Abaqus documentation) در مورد حلگر Abaqus/Standard را مرور کنیم:

Abaqus/Standard: is a general-purpose analysis product (solver) that can solve a wide range of linear and nonlinear problems involving the static, dynamic, thermal, electrical, and electromagnetic response of components. Abaqus/Standard solves a system of equations implicitly at each solution “increment.” In contrast, Abaqus/Explicit marches a solution forward through time in small time increments without solving a coupled system of equations at each increment (or even forming a global stiffness matrix). Abaqus/Standard is ideal for static and low-speed dynamic events where highly accurate stress solutions are important.

بر خلاف حلگر Explicit که مناسب دسته‌ای خاص از مسائل (دینامیک گذارا و شکل‌دهی) است، حلگر Implicit یک حلگر همه منظوره (general-purpose) است که برای شبیه سازی طیف گسترده‌ای از مسائل خطی و غیرخطی بکار گرفته می‌شود. بنابراین از حلگر Implicit می‌توان در مسائل استاتیک، دینامیک (با سرعت پایین)، انتقال حرارت، الکتریسیته و الکترومغناطیس استفاده کرد.

همانطور در پیش‌تر بیان شد، در حلگر Implicit در هر increment (نمو) تلاش‌های (iteration) متعددی برای حل معادلات تعادل می‌شود. در حالی که در حلگر Explicit نیازی به حل دستگاه معادلات نیست.

مقایسه حلگر Abaqus/Explicit با حلگر Abaqus/Standard

حلگر Abaqus/Standard یک حلگر general-purpose است که قادر به حل طیف گسترده از مسائل که دینامیک شدید و تماس‌های پیچیده ندارند، است. این در حالی است که حلگر Abaqus/Explicit مختص مسائل دینامیک با سرعت بالا مانند برخورد و مسائلی با روابط غیرخطی به شدت پیچیده مانند مسائل شکل‌دهی است.

نویسنده:
مهندس میلاد وحیدیان 

دانشجوی دکترای مهندسی مکانیک دانشگاه تهران

(برای مطالعه بیشتر روی نام یا تصویر ایشان کلیک کنید)