ارتعاشات مکانیکی (Mechanical Vibrations) به نوسانات (Oscillations) یا حرکات مکرر (Repetitive Motions) یک سیستم مکانیکی نسبت به موقعیت تعادلش اشاره دارد. مرحله نخست تحلیل سیستمهای ارتعاشی، مدل سازی آن است. مدل سازی سیستمها (Systems modeling) یعنی:
معادل سازی یک سیستم با سیستمی فرضی (مفهومی) سادهتر برای استخراج روابط ریاضی حاکم بر آن سیستم. در این معادل سازی معمولا فرضیات ساده کنندهای در نظر گرفته میشود.
در این مقاله قصد داریم به مدلسازی سیستمهای ارتعاشی (Modeling of Vibrating systems) بپردازیم.
- مراحل تحلیل یک سیستم ارتعاشی (Analyzing a Vibratory System)
- مدلسازی گسسته سیستمهای ارتعاشی (Discrete Modeling of Vibrating Systems)
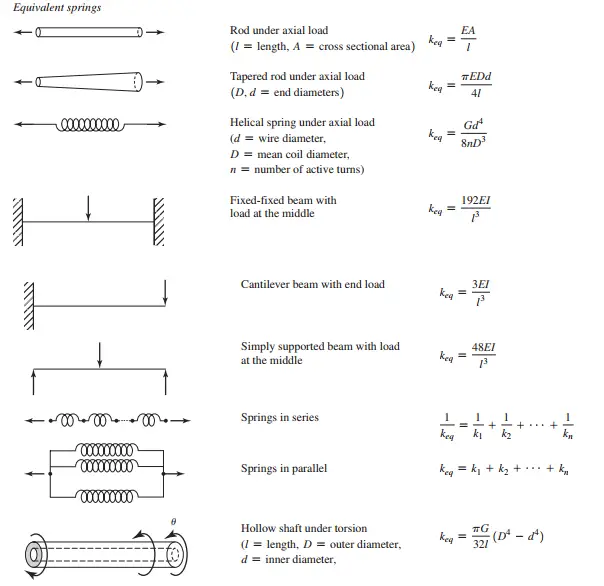
- المانهای متداول سیستمهای ارتعاشی گسسته
- المان سفتی الاستیک (Elastic Stiffness Element)
- فنرهای خطی (Linear Springs)
- فنرهای غیرخطی (Non-linear Springs)
- خطیسازی فنر غیرخطی (Linearization of a Nonlinear Spring)
- ثابتهای فنری المان الاستیک (Spring Constants of Elastic Elements)
- ترکیب فنرها (Combination of Springs)
- مثال: ثابت فنر معادل برای جرثقیل (Equivalent Spring Constant of a Crane)
- المان اینرسی (Inertia Element)
- المان میرایی (Damping Element)
- میرایی ویسکوز (Viscous Damping)
- ساخت دمپرهای ویسکوز (Construction of Viscous Dampers)
- میرایی کولمب یا اصطکاک خشک (Coulomb or Dry-Friction Damping)
- میرایی مواد یا میرایی جامد یا میرایی هیسترتیک (Material or Solid or Hysteretic Damping)
- ثابتهای معادل فنر و دمپر برای ماشین ابزار (Equivalent Spring and Damping Constants of a Machine Tool Support)
- مدلسازی چکش آهنگری: یک مثال کاربردی
- مدلسازی ریاضی موتور سیکلت: یک مثال کاربردی
مراحل تحلیل یک سیستم ارتعاشی (Analyzing a Vibratory System)
مرحله اول: مدلسازی سیستم (System Modeling)
مدلسازی ریاضی اولین و اساسیترین مرحله در تحلیل ارتعاشات است. هدف از این مرحله، ارائه یک مدل ریاضی از سیستم است که تمام ویژگی های اصلی سیستم را در بر میگیرد. مدل ریاضی باید جزئیات کافی را در بر داشته باشد تا بتوان سیستم را از طریق معادلات (بدون اینکه بیش از حد پیچیده شود) توصیف کرد.
در صورتی پارامترهای سیستم به صورت متمرکز یا تودهای (lumped) مدلسازی شود، سیستم ارتعاشی را سیستمی گسسته (discrete) میگویند و درصورتی که پارمترهای سیستم به صورت پیوسته (continuous) یا توزیع شده (distributed) مدلسازی شود، سیستم را پیوسته (continuous) میگویند.
در اصل تمامی سیستمهای ارتعاشی پیوسته (continuous) هستند که در برخی مسائل و تحلیلها میتواند سیستمهای ارتعاشی پیوسته (continuous) را با سیستمی گسسته (discrete) تقریب زد. مدلسازی گسسته (discrete) سیستمها، معادلات دیفرانسیل حاکم را از PDE به ODE تقلیل میدهد. این تقریب یا معادل سازی، امکان حل سریع و ساده مسئله را فراهم میکنند. هرچند گاهی اوقات مدلهای پیوسته ویژگیهایی از سیستم را نشان میدهند که با مدلهای گسسته معادل شده آن قابل پیشبینی نیستند.
مرحله دوم: استخراج معادلات حاکم (Deriving Governing Equations)
پس از مدلسازی ریاضی، مرحله بعدی استخراج معادلات حاکم (Governing Equations) یا معادلات حرکت (Equations of Motion) است. معادلات حاکم معمولاً به صورت معادلات دیفرانسیل هستند که رفتار دینامیکی سیستم را تحت شرایط ورودی مشخص توصیف میکنند. معادلات حاکم (Governing Equations) یا معادلات حرکت (Equations of Motion) با استفاده از قوانین فیزیکی به خصوص معادلات ممنتوم خطی (linear momentum) و معادلات ممنتوم زاویهای (angular momentum) استخراج میشوند.
در صورتی پارامترهای سیستم به صورت متمرکز یا تودهای (lumped) مدلسازی شود، سیستم ارتعاشی را سیستمی گسسته میگویند و معادلات دیفرانسل معمولی بر سیستم حاکم است. اگر پارمترهای سیستم به صورت پیوسته (continuous) یا توزیع شده (distributed) مدلسازی شود، سیستم را پیوسته (continuous) میگویند و معادلات دیفرنسیل با مشتقات جزئی بر سیستم حاکم است.
مرحله سوم: حل معادلات حاکم (Solving the Governing Equations)
پس از استخراج معادلات حاکم (Governing Equations) یا معادلات حرکت (Equations of Motion) مرحله بعدی حل این معادلات است. برای یافتن پاسخ سیستم به تحریکات خارجی، معادلات حاکم باید حل شوند. حل این معادلات به مهندسان امکان میدهد تا رفتار دینامیکی سیستم را در شرایط مختلف تحلیل کنند. به طور کلی، سه رویکرد برای حل معادلات حرکت (Equations of Motion) یک سیستم وجود دارد:
- روشهای تحلیلی (Analytical Methods)
- روشهای نیمهتحلیلی (Semi-Analytical Methods)
- روشهای عددی (Numerical Methods)
روشهای تحلیلی (Analytical Methods)
روشهای تحلیلی شامل یافتن راهحلهای دقیق و بسته برای معادلات دیفرانسیل حاکم بر سیستم است. این روشها معمولاً برای سیستمهای ساده و خطی قابل استفاده هستند. برخی از روشهای تحلیلی معمول عبارتند از:
- روش جداسازی متغیرها (Separation of Variables): این روش برای حل معادلات دیفرانسیل جزئی که به دو یا چند معادله دیفرانسیل معمولی قابل تجزیه هستند، استفاده میشود.
- روش لاپلاس (Laplace Transform): این روش با استفاده از تبدیل لاپلاس برای تبدیل معادلات دیفرانسیل به معادلات جبری که به سادگی قابل حل هستند، استفاده میشود.
روشهای نیمهتحلیلی (Semi-Analytical Methods)
روشهای نیمهتحلیلی، روشهایی هستند که ترکیبی از روشهای تحلیلی و عددی را برای یافتن راهحل معادلات دیفرانسیل استفاده میکنند. این روشها برای برخی سیستمهای پیچیدهتر و غیرخطی مناسب هستند. برخی از روشهای نیمهتحلیلی معمول عبارتند از:
- روش ناویر (Navier Method): این روش برای تحلیل ارتعاشات تیر ها, صفحات و پوستهها استفاده میشود. در این روش، معادلات حرکت با استفاده از سریهای توانی یا سایر توابع تقریبی حل میشوند. این روش حل تنها برای شرایط تکیه گاه ساده کاربردی می باشد.
- روش فوریه (Fourier Method): این روش برای تجزیه و تحلیل معادلات دیفرانسیل با استفاده از سریهای فوریه و تبدیلهای فوریه استفاده میشود.
- روش سریهای توانی (Power Series Method): در این روش، راهحل معادله به صورت یک سری توانی نمایش داده میشود و ضرایب سری با استفاده از شرایط مرزی تعیین میشوند.
- روش اختلالی (Perturbation Method): این روش برای حل معادلات دیفرانسیل غیرخطی با استفاده از توسعه راهحل به صورت سریهایی از یک پارامتر کوچک استفاده میشود.
- روش ریتز-گالرکین (Ritz-Galerkin Method): این روش برای تقریب معادلات دیفرانسیل با استفاده از توابع پایه و وزندهی گالرکین استفاده میشود.
روشهای عددی (Numerical Methods)
روشهای عددی برای حل معادلات دیفرانسیل که به صورت تحلیلی یا نیمهتحلیلی قابل حل نیستند، استفاده میشوند. این روشها با استفاده از الگوریتمهای کامپیوتری و تکنیکهای محاسباتی برای تقریب راهحل معادلات دیفرانسیل به کار میروند. برخی از روشهای عددی معمول عبارتند از:
- روش اویلر (Euler Method): این روش یکی از سادهترین روشهای عددی برای حل معادلات دیفرانسیل معمولی است.
- روش رانچ-کوتا (Runge-Kutta Method): این روش شامل مجموعهای از تکنیکهای عددی با دقت بالا برای حل معادلات دیفرانسیل معمولی است.
- روش تفاضل محدود (Finite Difference Method): این روش برای تقریب معادلات دیفرانسیل جزئی با استفاده از شبکههای محاسباتی و تفاضلهای محدود استفاده میشود.
- روش المان محدود (Finite Element Method): این روش برای تحلیل سیستمهای پیچیده با تقسیم سیستم به المان ها کوچکتر و حل معادلات دیفرانسیل برای هر المان استفاده میشود.
مرحله چهارم: تفسیر نتایج (Interpreting the Results)
مرحله نهایی در تحلیل ارتعاشات، تفسیر نتایج است. نتایج بدست آمده که معمولا جابجاییها (Displacements)، سرعتها (Velocities) و شتابها (Accelerations) در نقاط مختلف سیستم هستند را تحت شرایط مختلف تحلیل میکنیم. این تحلیل و بررسی شامل بررسی پایداری، پاسخ فرکانسی، و تاثیرات عوامل مختلف بر سیستم است. همچنین ممکن است نیاز به بررسی نتایج با دادههای تجربی باشد تا صحت و دقت مدل و تحلیل تایید شود.
در نهایت این تحلیلها به مهندسان کمک میکند تا فرکانسهای بحرانی و وضعیتهای خطرناک سیستم را شناسایی کرده و اقدامات لازم را انجام دهند. این تحلیلها به بهبود عملکرد و ایمنی سیستم کمک میکنند.
مدلسازی گسسته سیستمهای ارتعاشی (Discrete Modeling of Vibrating Systems)
در صورتی پارامترهای سیستم به صورت متمرکز یا تودهای (lumped) مدلسازی شود، سیستم ارتعاشی را سیستمی گسسته میگویند و معادلات دیفرانسل معمولی بر سیستم حاکم است. در اصل تمامی سیستمهای پیوسته (continuous) هستند اما میتواند در برخی مسائل آنهای به صورت سیستم گسسته مدل کرد.
مدلسازی گسسته سیستمهای ارتعاشات موجب میشود تا معادلات حاکم بر سیستم معادلات دیفرانسیل معمولی (ODE = Ordinary Differential Equations) که حل و تحلیل آن به مراتب از سیستمهای پیوسته با معادلات دیفرانسیل با مشتقات جزئی (PDE = Partial Differential Equations) سادهتر است.
سیستمهای گسسته با استفاده از خواص سفتی (stiffens) موثر، اینرسی (inertia) موثر و دمپینگ (damping) موثر آن مدلسازی میشوند.
المانهای متداول سیستمهای ارتعاشی گسسته
المان سفتی الاستیک (Elastic Stiffness Element)
در این بخش به بررسی المان سفتی الاستیک (فنری) در سیستمهای ارتعاشی می پردازیم. فنرها یکی از مهمترین اجزای سیستمهای مکانیکی و ارتعاشی هستند که برای ذخیره و آزاد کردن انرژی مکانیکی استفاده میشوند. در اینجا به تفصیل در مورد انواع مختلف فنرها و خواص آنها صحبت میکنیم.
فنرهای خطی (Linear Springs)
فنرهای خطی به گونهای طراحی شدهاند که نیروی بازگرداننده آنها نسبت به تغییر مکان، خطی است. به عبارت دیگر، رابطه نیرو-جابجایی در این فنرها به صورت خطی است:
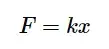
که در آن 𝐹 نیروی اعمال شده، 𝑘 ثابت سختی فنر و 𝑥 تغییر مکان است. ثابت سختی فنر، نیروی لازم برای ایجاد یک واحد تغییر مکان در فنر می باشد. در فنرهای خطی، نمودار نیرو-جابجایی یک خط راست است و انرژی ذخیره شده در فنر به صورت زیر محاسبه میشود:
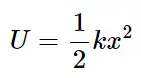
فنرهای غیرخطی (Non-linear Springs)
بیشتر فنرهای مورد استفاده در سیستمهای عملی، غیرخطی هستند، به خصوص وقتی که تغییر مکانها بزرگ باشند. در فنرهای غیرخطی، رابطه نیرو-جابجایی به صورت خطی نیست و میتواند به شکلهای مختلفی باشد. به عنوان مثال، نیروی بازگرداننده میتواند به صورت چندجملهای از جابجایی باشد:
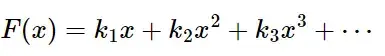
که در آن 𝑘1، 𝑘2، 𝑘3 و غیره ضرایب سختی هستند. این نوع فنرها به دلیل خصوصیات غیرخطی خود، در سیستمهایی که دارای تغییرات بزرگ در جابجایی هستند، مورد استفاده قرار میگیرند. یکی از مزایای استفاده از فنرهای غیرخطی، توانایی آنها در جذب و میرا کردن انرژی ارتعاشات بزرگتر است.
خطیسازی فنر غیرخطی (Linearization of a Nonlinear Spring)
در بسیاری از تحلیلهای مهندسی، برای سادهسازی مسئله، فنرهای غیرخطی خطیسازی میشوند. خطیسازی به معنای تقریب زدن رفتار غیرخطی فنر با یک رفتار خطی در یک ناحیه کوچک حول یک نقطه کاری است. این کار معمولاً با استفاده از بسط تیلور انجام میشود.
برای خطیسازی فنر غیرخطی 𝐹(𝑥) حول نقطه 𝑥0 ، توسط بسط تیلور مرتبه اول به صورت زیر بازنویسی می شود:
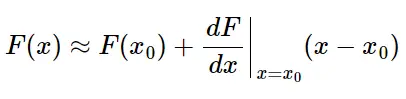
اگر نقطه 𝑥0 را صفر در نظر بگیریم (یعنی حول نقطه تعادل خطیسازی کنیم)، معادله به صورت زیر ساده میشود:
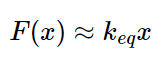
که در آن 𝑘𝑒𝑞 مشتق 𝐹(𝑥) نسبت به 𝑥 در نقطه 𝑥=0 است:
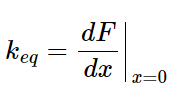
بنابراین، 𝑘𝑒𝑞 یک ثابت سختی معادل برای فنر غیرخطی است که در تحلیلهای خطی به کار میرود. این خطیسازی باعث میشود که تحلیل سیستمهای پیچیده سادهتر شده و بتوان از روشهای استاندارد تحلیل سیستمهای خطی استفاده کرد.
کاربردهای خطیسازی
خطیسازی فنرهای غیرخطی در بسیاری از موارد مفید است، از جمله:
- طراحی سیستمهای تعلیق خودرو: در طراحی سیستمهای تعلیق خودرو، از فنرهای غیرخطی استفاده میشود. خطیسازی این فنرها در تحلیل رفتار سیستم تعلیق تحت بارهای مختلف کمک میکند.
- تحلیل ارتعاشات سازههای بزرگ: در سازههای بزرگ مانند پلها و ساختمانها، استفاده از فنرهای غیرخطی برای کنترل ارتعاشات متداول است. خطیسازی این فنرها میتواند فرآیند تحلیل را سادهتر و دقیقتر کند.
- سیستمهای کنترل ارتعاشات صنعتی: در تجهیزات صنعتی که نیاز به کنترل دقیق ارتعاشات دارند، فنرهای غیرخطی به کار میروند. خطیسازی این فنرها به مهندسان اجازه میدهد تا با استفاده از روشهای تحلیلی و عددی، عملکرد سیستم را به سادگی تحلیل کنند.
محدودیتهای خطیسازی
در حالی که خطیسازی یک ابزار قدرتمند برای سادهسازی تحلیل است، باید توجه داشت که این روش دارای محدودیتهایی نیز هست:
- دقت محدود: خطیسازی تنها در نواحی کوچک حول نقطه تعادل دقت بالایی دارد و در جابجاییهای بزرگتر ممکن است نتایج دقیق نباشند.
- عدم توانایی در مدلسازی رفتار پیچیده: بسیاری از رفتارهای غیرخطی فنرها، مانند هیسترزیس و اثرات غیراشباع، با خطیسازی قابل مدلسازی نیستند.
- تکیه بر فرضیات سادهساز: خطیسازی معمولاً بر اساس فرضیاتی سادهساز انجام میشود که ممکن است در همه شرایط واقعی معتبر نباشند.
ثابتهای فنری المان الاستیک (Spring Constants of Elastic Elements)
ثابتهای فنری المان الاستیک به میزان سختی یا نرمی این المان ها بستگی دارد. این ثابتها نشاندهنده نیروی لازم برای ایجاد یک واحد تغییر مکان در المان فنری هستند. ثابتهای فنری المان ها الاستیک میتوانند به صورت تجربی یا تئوری تعیین شوند.
برای مثال، در یک میله تحت کشش یا فشار، ثابت فنری به صورت زیر محاسبه میشود:
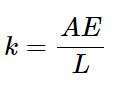
که در آن 𝐴 سطح مقطع، 𝐸 مدول الاستیسیته و 𝐿 طول میله است.
ترکیب فنرها (Combination of Springs)
در بسیاری از کاربردهای عملی، چندین فنر خطی به صورت ترکیبی استفاده میشوند. این فنرها میتوانند به صورت موازی یا سری با هم ترکیب شوند.
فنرهای موازی (Springs in Parallel)
وقتی چندین فنر به صورت موازی به هم متصل شوند، سختی معادل آنها به صورت جمع سختیهای تک تک فنرها محاسبه میشود. برای دو فنر با ثابتهای سختی 𝑘1 و 𝑘2:
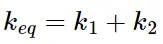
فنرهای سری (Springs in Series)
وقتی چندین فنر به صورت سری به هم متصل شوند، سختی معادل آنها به صورت معکوس جمع معکوس سختیهای تک تک فنرها محاسبه میشود. برای دو فنر با ثابتهای سختی 𝑘1 و 𝑘2:
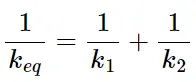
مثال: ثابت فنر معادل برای جرثقیل (Equivalent Spring Constant of a Crane)
در این مثال، هدف یافتن ثابت فنر معادل یک سیستم جرثقیل است. برای این کار، انرژی پتانسیل ذخیره شده در فنرها مورد بررسی قرار میگیرد و ثابت فنر معادل محاسبه میشود.
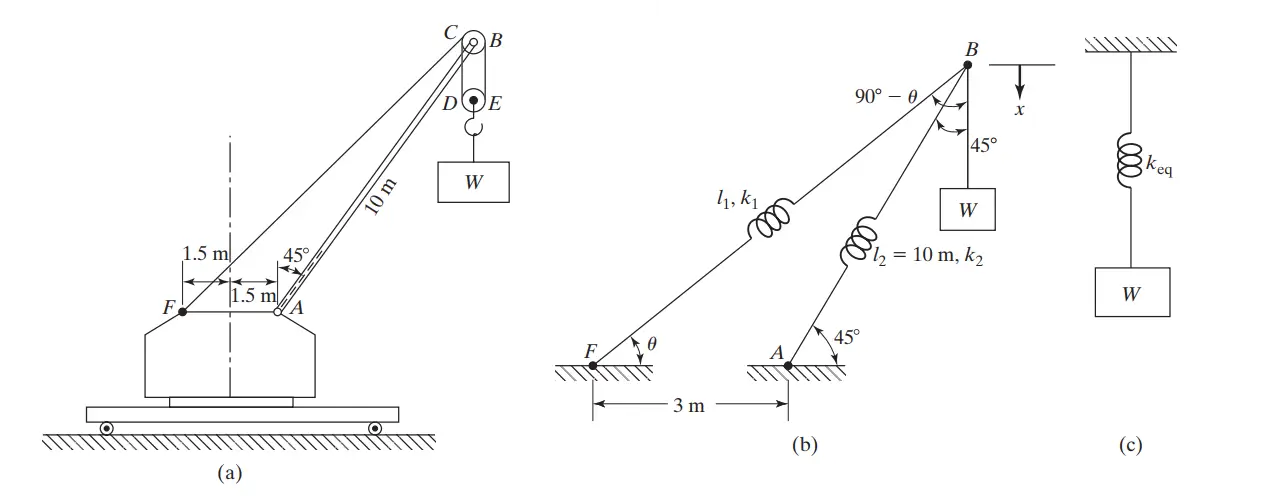
مدلسازی سیستم جرثقیل
سیستم جرثقیل شامل بازوی جرثقیل و کابلهای متصل به آن است. در این تحلیل، فرض میشود که پایه جرثقیل صلب است و کابل و بازوی جرثقیل به ترتیب در نقاط ثابت شدهاند. اثر کابلهای متصل به بازوی جرثقیل نادیده گرفته میشود و وزن بار به صورت مستقیم به نقطه خاصی از بازو اعمال می شود.
جابجایی عمودی نقطه انتهایی بازو باعث تغییر شکل فنرهای مختلف سیستم میشود. در این حالت، جابجایی نقطه 𝐵 باعث تغییر شکل بازو و کابل به میزانهای مختلفی میشود. جابجایی بازو به میزان 𝑥2=𝑥cos45 و جابجایی فنر کابل به میزان 𝑥1=𝑥cos(90−𝜃) خواهد بود.
محاسبه ثابتهای فنر
برای محاسبه ثابتهای بازو و کابل، از فرمولهای زیر استفاده میشود:
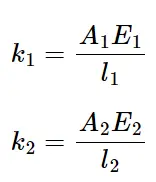
که در آن:
- 𝐴 مساحت سطح مقطع
- 𝐸 مدول یانگ
- 𝑙 طول عضو مورد نظر
محاسبه انرژی پتانسیل سیستم
انرژی پتانسیل ذخیره شده در فنرهای سیستم به صورت زیر محاسبه میشود:
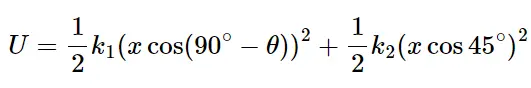
با قرار دادن مقادیر 𝜃 و مقادیر مربوط به k1 و k2 در این معادله، میتوان انرژی پتانسیل کل سیستم را به دست آورد.
محاسبه ثابت فنر معادل
ثابت فنر معادل سیستم در جهت عمودی به صورتی محاسبه میشود که انرژی پتانسیل معادل آن برابر با انرژی پتانسیل کل سیستم باشد:
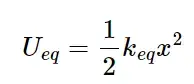
با قرار دادن Ueq، ثابت فنر معادل به صورت زیر به دست میآید:
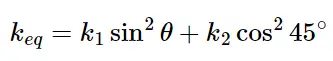
با جایگذاری مقادیر 𝜃 و زاویهها، ثابت فنر معادل نهایی به دست خواهد آمد.
المان اینرسی (Inertia Element)
المان جرمی یا اینرسی به عنوان یک جسم صلب فرض میشود که میتواند با تغییر سرعت خود، انرژی جنبشی سبستم را افزایش یا کاهش دهد. طبق قانون دوم نیوتن، حاصلضرب جرم در شتاب آن برابر با نیروی اعمالشده به جرم است. کار انجامشده برابر با حاصلضرب نیرو در جابجایی در جهت نیرو است و کار انجامشده بر روی یک جرم به صورت انرژی جنبشی در جرم ذخیره میشود.
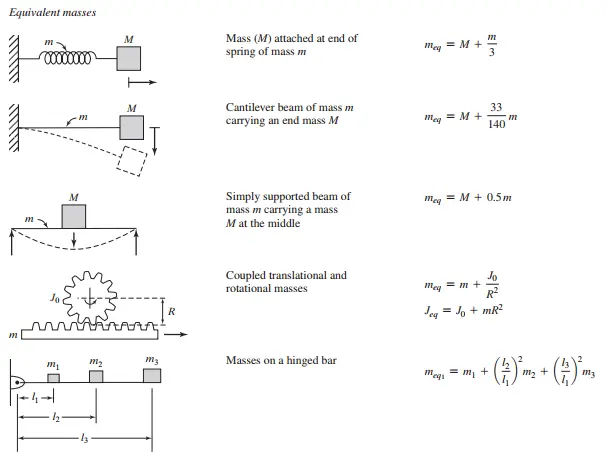
در اکثر موارد، ما باید از یک مدل ریاضی برای نمایش سیستم ارتعاشی واقعی استفاده کنیم و معمولاً مدلهای مختلفی وجود دارد. هدف تحلیل معمولاً تعیین میکند که کدام مدل ریاضی مناسب است. پس از انتخاب مدل، المان ها جرمی یا اینرسی سیستم به راحتی قابل تشخیص هستند. به عنوان مثال، یک مدل ساده شده از ساختمان با یک جرم انتهایی را در نظر بگیرید که در شکل نشان داده شده است. برای یک تحلیل سریع و نسبتاً دقیق، جرم و میرایی تیر را میتوان نادیده گرفت و سیستم را به عنوان یک سیستم جرم-فنر مدلسازی کرد. جرم نوک تیر نمایانگر المان جرمی است و الاستیسیته تیر نمایانگر سختی فنر است.
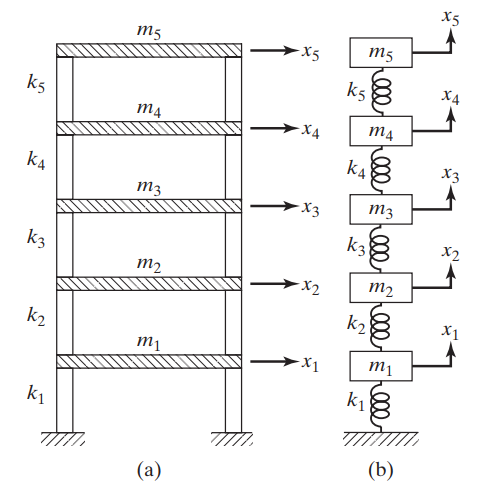
جرمهای متمرکز و پیوسته (Lumped and Distributed Masses)
در مدلسازی سیستمهای ارتعاشی، جرمها میتوانند به صورت نقطهای یا پیوسته در نظر گرفته شوند. جرم نقطهای به یک جرم متمرکز در یک نقطه خاص از سیستم اشاره دارد، در حالی که جرم پیوسته به جرمهایی اشاره دارد که در طول یک بخش از سیستم پخش شدهاند. انتخاب نوع جرم بستگی به نیاز دقت مدل و سادگی تحلیل دارد.
جرم متمرکز (Lumped Masses)
جرمهای نقطهای برای سادهسازی مدلسازی سیستمهای پیچیده استفاده میشوند. در این مدل، فرض میشود که تمام جرم سیستم در چند نقطه خاص متمرکز است. این نوع مدلسازی در بسیاری از کاربردهای عملی برای تحلیل ارتعاشات سازههای ساده استفاده میشود.
جرم توزیع شده (Distributed Masses)
در مواردی که دقت بالاتری مورد نیاز است، جرمهای پیوسته در نظر گرفته میشوند. در این مدل، جرم در طول یک بخش از سیستم به طور یکنواخت توزیع شده است. این نوع مدلسازی برای تحلیل ارتعاشات سازههای پیچیده مانند پلها و ساختمانها استفاده میشود.
انرژی جنبشی (Kinetic Energy)
انرژی جنبشی یک جرم تابعی از جرم و سرعت آن است. برای یک جرم نقطهای، انرژی جنبشی به صورت زیر تعریف میشود:
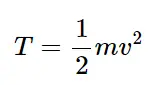
که در آن 𝑚 جرم و 𝑣 سرعت است. در سیستمهای با جرم پیوسته، انرژی جنبشی به صورت انتگرالی از سرعت در طول سیستم محاسبه میشود.
انرژی جنبشی در سیستمهای جرم نقطهای (Kinetic Energy in Lumped Mass Systems)
برای سیستمهای با جرم نقطهای، انرژی جنبشی هر جرم نقطهای به صورت مجزا محاسبه شده و سپس با هم جمع میشود. به عنوان مثال، در یک سیستم دو درجه آزادی، انرژی جنبشی به صورت زیر است:
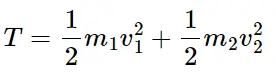
انرژی جنبشی در سیستمهای جرم پیوسته (Kinetic Energy in Distributed Mass Systems)
برای سیستمهای با جرم پیوسته، انرژی جنبشی به صورت انتگرالی محاسبه میشود. به عنوان مثال، برای یک تیر با جرم پیوسته یکنواخت، انرژی جنبشی به صورت زیر است:
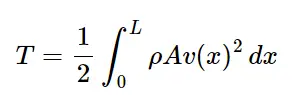
که در آن 𝜌 چگالی، 𝐴 سطح مقطع و 𝑣(𝑥) سرعت در نقطه 𝑥 از طول تیر 𝐿 است.
انتخاب مدل ریاضی (Choosing the Mathematical Model)
انتخاب مدل ریاضی مناسب برای تحلیل ارتعاشات بستگی به پیچیدگی سیستم و نیاز دقت دارد. برای سیستمهای ساده، مدلهای جرم نقطهای معمولاً کافی هستند، در حالی که برای سیستمهای پیچیدهتر، مدلهای جرم پیوسته نیاز به تحلیل دقیقتر دارند. در بسیاری از موارد، ترکیبی از هر دو نوع مدل برای دستیابی به دقت و سادگی مورد استفاده قرار میگیرد.
المان میرایی (Damping Element)
در بسیاری از سیستمهای عملی، انرژی ارتعاشی به تدریج به حرارت یا صدا تبدیل میشود. به دلیل کاهش انرژی، پاسخ سیستم مانند جابجایی به تدریج کاهش مییابد. مکانیزمی که از طریق آن انرژی ارتعاشی به تدریج به حرارت یا صدا تبدیل میشود، میرایی نامیده میشود. اگرچه مقدار انرژی تبدیل شده به حرارت یا صدا نسبتاً کوچک است، در نظر گرفتن میرایی برای پیشبینی دقیق پاسخ ارتعاشی سیستم اهمیت دارد. فرض میشود دمپرها نه جرم دارند و نه خاصیت الاستیسیته، و نیروی میرایی فقط در صورتی وجود دارد که بین دو انتهای دمپر سرعت نسبی وجود داشته باشد. تعیین علل میرایی در سیستمهای عملی دشوار است. از این رو، میرایی به صورت یک یا چند نوع از انواع زیر مدلسازی میشود.
میرایی ویسکوز (Viscous Damping)
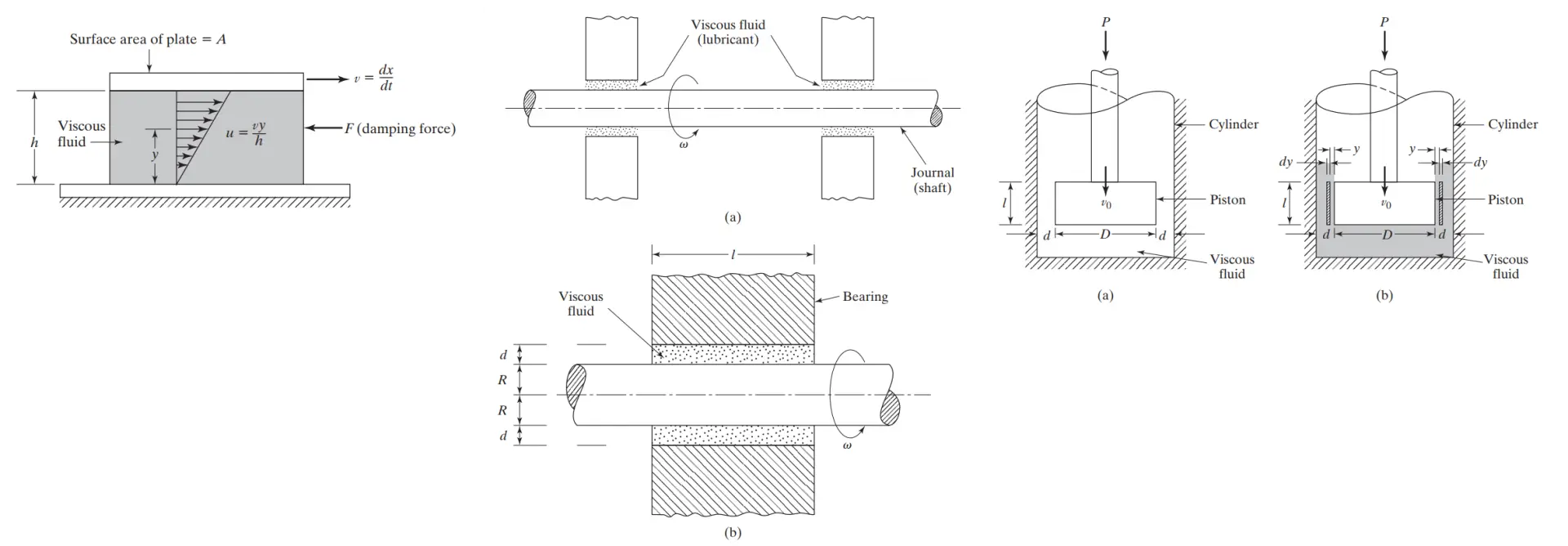
میرایی ویسکوز رایجترین مکانیزم میرایی در تحلیل ارتعاشات است. هنگامی که سیستمهای مکانیکی در یک محیط سیال مانند هوا، گاز، آب یا روغن ارتعاش میکنند، مقاومت سیال به جسم متحرک باعث اتلاف انرژی میشود. در این حالت، مقدار انرژی اتلاف شده به عوامل زیادی بستگی دارد، مانند اندازه و شکل جسم مرتعش، ویسکوزیته سیال، فرکانس ارتعاش و سرعت جسم مرتعش. در میرایی ویسکوز، نیروی میرایی متناسب با سرعت جسم مرتعش است. مثالهای معمول میرایی ویسکوز عبارتند از:
- فیلم سیال بین سطوح لغزنده
- جریان سیال اطراف پیستون در یک سیلندر
- جریان سیال از طریق یک روزنه
- فیلم سیال اطراف یک ژورنال در یک یاتاقان
ساخت دمپرهای ویسکوز (Construction of Viscous Dampers)
دمپرهای ویسکوز میتوانند به روشهای مختلفی ساخته شوند. به عنوان مثال، هنگامی که یک صفحه نسبت به صفحه موازی دیگر با یک سیال ویسکوز بین صفحات حرکت میکند، یک دمپر ویسکوز به دست میآید. در زیر مثالهایی برای روشهای مختلف ساخت دمپرهای ویسکوز در کاربردهای مختلف آورده شده است.
دمپرهای ویسکوز به روشهای مختلفی ساخته میشوند. به عنوان مثال، یک دمپر ویسکوز میتواند از حرکت یک صفحه نسبت به یک صفحه موازی دیگر با یک سیال ویسکوز بین آنها به دست آید. نمونههایی از روشهای ساخت دمپرهای ویسکوز در کاربردهای مختلف شامل موارد زیر است:
- جریان سیال از طریق یک روزنه
- حرکت پیستون در سیلندر پر از سیال ویسکوز
- یاتاقانهای ژورنال با سیال ویسکوز
میرایی کولمب یا اصطکاک خشک (Coulomb or Dry-Friction Damping)
در اینجا نیروی میرایی در بزرگی ثابت است اما در جهت مخالف حرکت جسم مرتعش است. این نوع میرایی به دلیل اصطکاک بین سطوح مالشی که یا خشک هستند یا دارای روانکاری ناکافی هستند، ایجاد میشود.
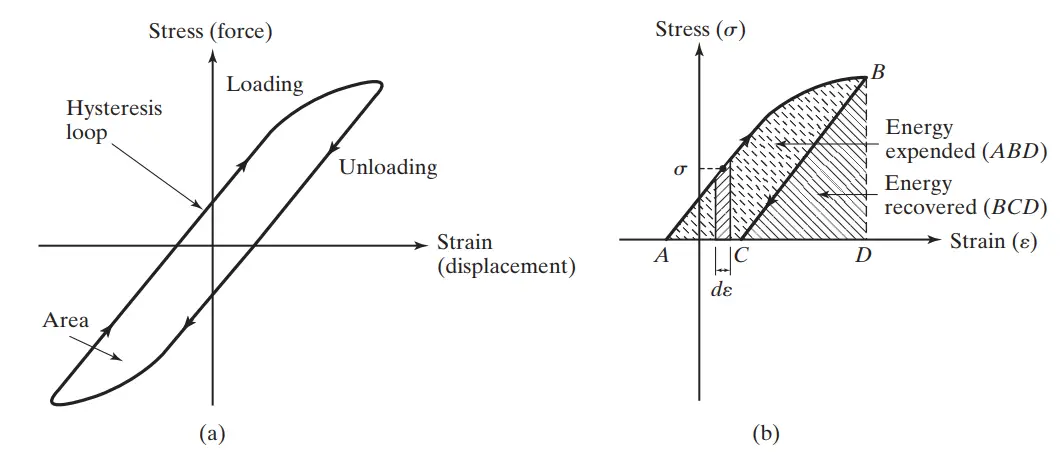
میرایی مواد یا میرایی جامد یا میرایی هیسترتیک (Material or Solid or Hysteretic Damping)
هنگامی که یک ماده تغییر شکل میدهد، انرژی توسط ماده جذب و اتلاف میشود. این اثر به دلیل اصطکاک بین صفحات داخلی ماده است که به هنگام تغییر شکل، بر روی یکدیگر سر میخورند یا لغزش میکنند. هنگامی که یک جسم دارای میرایی هیسترتیک تحت ارتعاش قرار میگیرد، نمودار تنش-کرنش یک حلقه هیسترزیست تشکیل می دهد. مساحت این حلقه نشاندهنده انرژی از دست رفته در هر واحد حجم از جسم در هر سیکل به دلیل میرایی ساختاری آن است.
ثابتهای معادل فنر و دمپر برای ماشین ابزار (Equivalent Spring and Damping Constants of a Machine Tool Support)
در این بخش، به بررسی ثابتهای معادل فنر و دمپر برای یک ماشین ابزار افقی پرداخته میشود. این مدل شامل فنرها و دمپرهای مختلفی است که در نقاط مختلف سیستم قرار گرفتهاند. هدف از این تحلیل، یافتن ثابتهای معادل برای فنر و دمپر سیستم به منظور سادهسازی تحلیل ارتعاشی است.
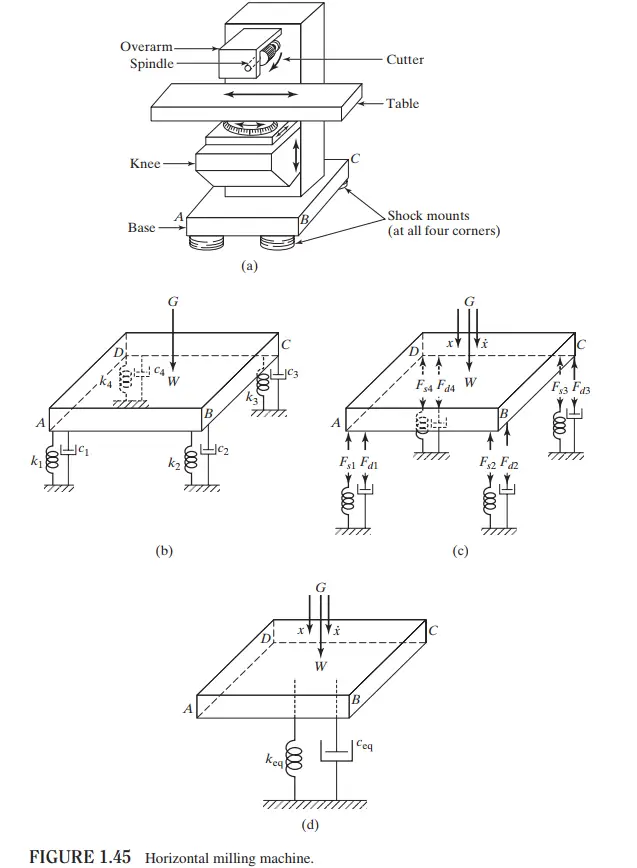
توضیح سیستم ماشین ابزار افقی
این سیستم شامل اجزای مختلفی است که به صورت زیر توضیح داده میشوند:
- بخش بالایی و اسپیندل (Overarm and Spindle): بخش بالایی ماشین ابزار که شامل اسپیندل و برشدهنده میباشد.
- میز (Table): میز ماشین ابزار که بر روی بخش میانی قرار دارد و میتواند در جهتهای مختلف حرکت کند.
- بخش میانی (Knee): بخش میانی ماشین ابزار که بین میز و پایه قرار دارد.
- پایه (Base): پایه ماشین ابزار که به زمین متصل است.
- تکیهگاههای ضربهگیر (Shock mounts): تکیهگاههایی که در چهار گوشه پایه قرار دارند و باعث کاهش ارتعاشات و شوکها میشوند.
مدل مکانیکی ماشین ابزار
برای مدلسازی مکانیکی این ماشین ابزار، چهار فنر و دمپر در نظر گرفته شده است که در چهار گوشه پایه قرار دارند. هر کدام از این فنرها و دمپرها خصوصیات ارتعاشی خاص خود را دارند که با 𝑘1,𝑐1;𝑘2,𝑐2;𝑘3,𝑐3;𝑘4;𝑐4 نمایش داده میشوند. این فنرها و دمپرها نمایانگر خصوصیات ارتعاشی پایه ماشین ابزار هستند.
برای یافتن ثابتهای معادل فنر و دمپر، ابتدا باید نیروهای وارد بر سیستم شناسایی شوند. این نیروها شامل وزن ماشین ابزار 𝑊 و نیروهای ارتعاشی در نقاط مختلف پایه میباشند. سپس با ترکیب این فنرها و دمپرها به صورت سری و موازی، میتوان ثابتهای معادل 𝑘𝑒𝑞 و 𝑐𝑒𝑞 را به دست آورد.
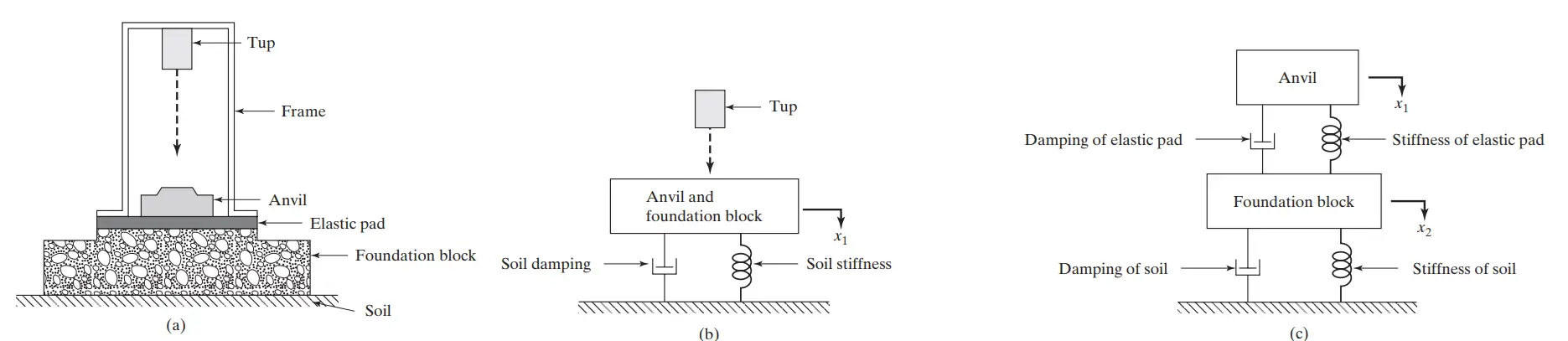
مدلسازی چکش آهنگری: یک مثال کاربردی
در این بخش، به بررسی مدلسازی ریاضی یک چکش آهنگری پرداخته میشود. این مدل شامل اجزای مختلفی است که هر یک دارای ویژگیهای ارتعاشی خاص خود هستند. هدف از این مدلسازی، تحلیل رفتار دینامیکی چکش آهنگری و شناسایی مناطق بحرانی آن است.
مدلسازی ریاضی (Mathematical Modeling)
در این مدل، چکش آهنگری به همراه پایه به عنوان یک سیستم ارتعاشی چند درجه آزادی (MDOF) مدلسازی میشود. اجزای اصلی مدل شامل موارد زیر است:
- پایه (Foundation Block and Anvil): این بخش به عنوان جرم اصلی سیستم در نظر گرفته میشود. پایه دارای جرم 𝑚𝑎𝑛𝑣𝑖𝑙 است که به وسیله پد الاستیک و خاک به زمین متصل شده است.
- پد الاستیک (Elastic Pad): پد الاستیک بین پایه و زمین قرار دارد و به عنوان یک فنر با سختی 𝑘𝑝𝑎𝑑 و میرایی 𝑐𝑝𝑎𝑑 عمل میکند.
- خاک (Soil): خاک زیر بلوک پایه قرار دارد و به عنوان یک دمپر و فنر با سختی 𝑘𝑠𝑜𝑖𝑙 و میرایی 𝑐𝑠𝑜𝑖𝑙 در نظر گرفته میشود.
- تپ (Tup): تپ چکش که به بلوک پایه ضربه میزند، به عنوان نیروی تحریک 𝐹(𝑡) وارد سیستم میشود.
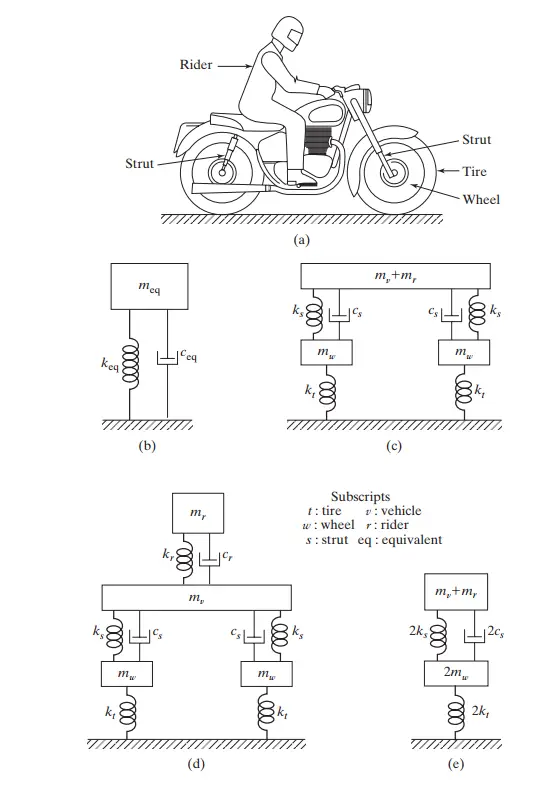
مدلسازی ریاضی موتور سیکلت: یک مثال کاربردی
در این بخش، به بررسی مدلسازی ریاضی یک موتور سیکلت به همراه راننده آن پرداخته میشود. این مثال شامل مراحل مختلف تحلیل ارتعاشات است که به شرح زیر بیان میشود:
مدلسازی ریاضی (Mathematical Modeling)
در این مرحله، ابتدا یک مدل ساده برای سیستم تعریف میشود. موتور سیکلت به همراه راننده به صورت یک سیستم یک درجه آزادی (Single-Degree-of-Freedom or SDOF) مدلسازی میشود. در این مدل:
- جرم معادل (Equivalent Mass): شامل جرم چرخها، بدنه موتور سیکلت و راننده است.
- سختی معادل (Equivalent Stiffness): شامل سختی تایرها، فنرها و راننده است.
- میرایی معادل (Equivalent Damping): شامل میرایی فنرها و راننده است.
استخراج معادلات حاکم (Deriving Governing Equations)
با استفاده از مدل ریاضی، معادلات حاکم بر سیستم استخراج میشود. در اینجا، معادله حرکت سیستم به صورت زیر بیان میشود:
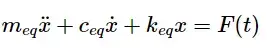
که در آن 𝑚𝑒𝑞 جرم معادل، 𝑐𝑒𝑞 میرایی معادل، 𝑘𝑒𝑞 سختی معادل و 𝐹(𝑡) نیروی ورودی به سیستم است.
تحلیل پاسخ سیستم (System Response Analysis)
پس از حل معادلات، پاسخ سیستم تحلیل میشود. پاسخ سیستم شامل جابجاییها، سرعتها و شتابها برای سیستم یک درجه آزادی ما است. این تحلیل به شناسایی مناطق بحرانی و وضعیتهای خطرناک کمک میکند.
مدلهای چند درجه آزادی (MDOF Models)
در مدلهای چند درجه آزادی (Multiple-Degree-of-Freedom or MDOF) ، سیستم به تعدادی از درجات آزادی تقسیم میشود که هر کدام میتواند به طور مستقل حرکت کند. این مدلها برای سیستمهای پیچیدهتر مانند ساختمانها، پلها و ماشینهای پیچیدهتر استفاده میشوند. هر درجه آزادی دارای جرم، سختی و میرایی خاص خود است و معادلات حرکت برای هر درجه آزادی نوشته میشود. برخی از تفاوت های اصلی بین مدل سازی سیستم های یک درجه و چند درجه آزادی را می توان به صورت زیر خلاصه کرد:
- سادگی مدلسازی: مدلهای SDOF سادهتر هستند و برای سیستمهای سادهتر مناسباند. مدلهای MDOF برای سیستمهای پیچیدهتر با چندین قسمت متحرک مناسب هستند.
- دقت تحلیل: مدلهای MDOF دقت بالاتری دارند زیرا جزئیات بیشتری از سیستم را در نظر میگیرند.
- هزینه محاسباتی: مدلهای SDOF نیاز به محاسبات کمتری دارند و سریعتر تحلیل میشوند، در حالی که مدلهای MDOF به محاسبات بیشتری نیاز دارند.
- کاربرد: مدلهای SDOF برای تحلیل اولیه و سریع مناسباند، در حالی که مدلهای MDOF برای تحلیلهای دقیقتر و طراحیهای پیشرفتهتر استفاده میشوند.