ارتعاشات مکانیکی (Mechanical Vibrations)

ارتعاشات مکانیکی (Mechanical Vibrations): اصول و مفاهیم پایه ارتعاشات

ارتعاشات مکانیکی (Mechanical Vibrations) به نوسانات (Oscillations) یا حرکات مکرر (Repetitive Motions) یک سیستم (سامانه) مکانیکی نسبت به موقعیت تعادلش اشاره دارد. این ارتعاشات می‌تواند در سیستم‌های مهندسی مختلف از جمله ماشین آلات، سازه ها، خودرو و هواپیما رخ دهد.

تاریخچه‌ای کوتاه از ارتعاشات (A Brief History of Vibrations)

مطالعه ارتعاشات مکانیکی (Mechanical Vibrations) قدمتی به عمر موسیقی و ایجاد اولین سازهای موسیقی توسط انسان دارد. فیثاغورس (Pythagoras) اولین کسی بود که صداهای موسیقی را به صورت علمی بررسی کرد و نشان داد که صداهای تولید شده توسط یک سیم مرتعش (Vibrating String) به طول سیم مرتبط هستند. گالیله (Galileo) با مطالعه پاندول (Pendulum) و سیم‌های مرتعش، پایه‌های علمی ارتعاشات را بنا نهاد.

در قرن بیستم، فراهام (Frahm) به اهمیت ارتعاشات پیچشی (Torsional Vibrations) در طراحی شفت‌های پروانه کشتی‌های بخار پی برد و جاذب ارتعاشات دینامیکی (Dynamic Vibration Absorber) را پیشنهاد داد. استودولا و د لاوال (Stodola, De Laval) نیز به مطالعه ارتعاشات تیرها و دیسک‌های چرخان پرداختند و راه‌حل‌های عملی برای تحلیل ارتعاشات این سیستم‌ها ارائه کردند.

مطالعات اخیر نشان داده‌اند که بسیاری از مشکلات سیستم های مکانیکی (Mechanical Systems) ناشی از رفتار غیرخطی (Nonlinear Behavior) آن ها هستند و پدیده‌هایی در سیستم‌های غیرخطی رخ می‌دهند که در سیستم‌های خطی از آن ها چشم پوشی می شوند. به همین دلیل تحلیل ارتعاشات غیر خطی (Nonlinear Vibration Analysis) به صورت چشم گیری مورد اهمیت قرار گرفته است.

همچنین، مفاهیم و روش‌های تحلیل ارتعاشات تصادفی (Random Vibration Analysis) برای پدیده‌های مختلفی مانند زلزله‌ها (Earthquakes) و نویز موتورهای جت (Jet Engine Noise) توسعه یافته‌اند که یکی از عوامل تخریب غیر قابل پیشبینی (Unpredictable Failure) سیستم‌ها را در بر می‌گیرد که به دوام سیستم‌های مکانیکی (Mechanical System Durability) و افزایش بازده آن ها کمک های بسیاری کرده است.

این پیشرفت‌ها باعث شده‌اند که نظریه ارتعاشات (Vibration Theory) به یکی از ابزارهای مهم در مهندسی تبدیل شود و کاربردهای گسترده‌ای در طراحی و تحلیل سیستم‌های مختلف پیدا کند.

چرا باید ارتعاشات یک سیستم برای ما اهمیت داشته باشد؟

ارتعاشات در بسیاری از جنبه‌های زندگی ما نقش مهمی ایفا می‌کنند. برای مثال، ما با ارتعاش پرده گوش خود (Eardrum Vibration) می‌شنویم، با ارتعاش امواج، نور را می‌بینیم، و حتی تنفس و راه رفتن ما نیز به نوعی با ارتعاشات همراه هستند. درک پدیده‌های ارتعاشی برای دانشمندان اهمیت بسیاری دارد. تلاش دانشمندان بر این بوده است که این پدیده های فیزیکی را به صورت مدل های ریاضی (Mathematical Models) ارایه دهند تا به کمک آنها بتوانند ابتدا سیستم های ارتعاشی (Vibratory Systems) را تحلیل و سپس سیستم های بهینه ارتعاشی طراحی کنند.

امروزه، مطالعه ارتعاشات به دلیل کاربردهای گسترده‌ای که در مهندسی دارند، از اهمیت ویژه‌ای برخوردار است. این کاربردها شامل طراحی ماشین‌ها (Machine Design)، سازه‌ها (Structures)، موتورها (Engines)، توربین‌ها (Turbines) و سیستم‌های کنترلی (Control Systems) می‌شوند.

بسیاری از ماشین‌آلات با مشکلات ارتعاشی مواجه هستند که ممکن است به دلیل عدم تعادل (Imbalance) در طراحی یا ساخت باشد. برای مثال چرخ‌های برخی از خودرو ها ممکن است در سرعت‌های بالا از مسیر خود منحرف شوند. یا در توربین‌ها، ارتعاشات می‌تواند باعث خرابی‌های مکانیکی قابل توجهی شود. علاوه بر این، سازه‌هایی که ماشین‌آلات سنگین یا موتورهای رفت و برگشتی (Reciprocating Engines) را تحمل می‌کنند نیز تحت تأثیر ارتعاشات قرار می‌گیرند و ممکن است به دلیل پدیده خستگی (Fatigue) ناشی از تغییرات دوره‌ای تنش تخریب شوند.

ارتعاشات همچنین باعث سایش سریع‌تر قطعات ماشین (Wear of Machine Parts)، ایجاد سر و صدا (Noise) و شل شدن اتصال‌دهنده‌ها (Loosening of Fasteners) می‌شود. در فرآیندهای برش فلزات (Metal Cutting Processes) نیز، ارتعاش می‌تواند منجر به لرزش (Chatter) و ایجاد سطحی ناهموار شود.

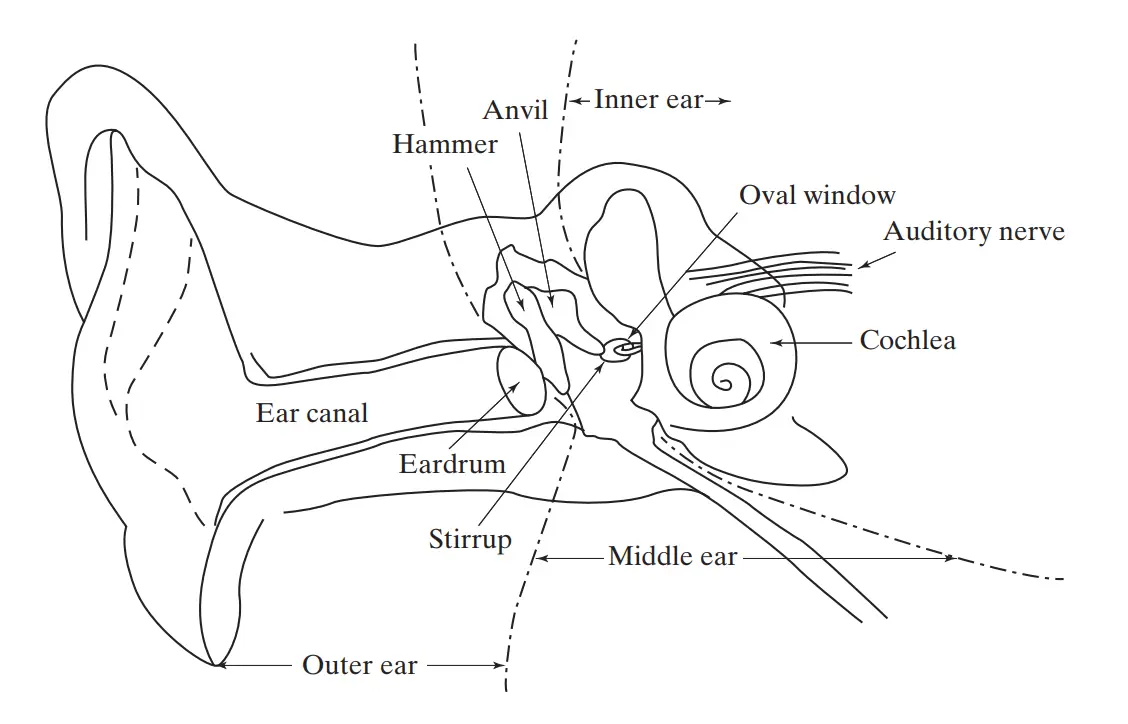
تبدیل ارتعاشات به صدا توسط گوش انسان

گوش انسان از سه بخش بیرونی، میانی و درونی تشکیل شده است. هنگامی که موج‌های فشاری ناشی از صدا یا موسیقی به پرده گوش برخورد می‌کنند، پرده گوش به ارتعاش درمی‌آید. این ارتعاشات از طریق استخوان‌های کوچک گوش میانی به گوش درونی منتقل می‌شوند. بخش اصلی گوش درونی که حلزون گوش (Cochlea) نام دارد، شامل دو محفظه پر از مایعی به نام پری‌لیمف (Perilymph) است که توسط غشای بازیلار (Basilar Membrane) از هم جدا شده‌اند. روی این غشا هزاران موی کوچک به نام سیلیا (Cilia) وجود دارد.

ارتعاشات از طریق مایع به غشای بازیلار منتقل شده و سپس به ایمپالس‌های الکتریکی (Electrical Impulses) تبدیل می‌شوند. این ایمپالس‌ها از طریق اعصاب شنوایی (Auditory Nerves) به مغز فرستاده می‌شوند و مغز آنها را به عنوان صدا تفسیر می‌کند. این فرآیند به ما امکان می‌دهد صداها را بشنویم و تشخیص دهیم.

مفاهیم پایه ارتعاشات (Basic Concenpts of Vibration)

ارتعاشات (Vibration) چیست؟

هر حرکتی که بعد از گذشت زمان معینی تکرار شود، ارتعاش (vibration) یا نوسان (oscillation) نامیده می‌شود. نوسان آونگ (Pendulum) و حرکت رفت و برگشتی جرم و فنر، نمونه‌های از ارتعاشات هستند. علم ارتعاشات به مطالعه حرکات نوسانی اجسام، پدید‌ها و نیروهای مرتبط با آن می‌پردازد.

اجزای اصلی سیستم‌های ارتعاشی (Elementary Parts of Vibrating Systems)

یک سیستم ارتعاشی به طور کلی شامل المانی برای ذخیره انرژی پتانسیل (فنر یا خاصیت الاستیک)، المانی برای ذخیره انرژی جنبشی (جرم یا لختی) و المانی برای اتلاف تدریجی انرژی (دمپر یا میراگر) است. ارتعاش یک سیستم شامل انتقال متناوب انرژی پتانسیل آن به انرژی جنبشی و بالعکس است. اگر سیستم دارای دمپینگ (میرائی) ارتعاش باشد، در هر چرخه ارتعاش بخشی از انرژی تلف می‌شود.

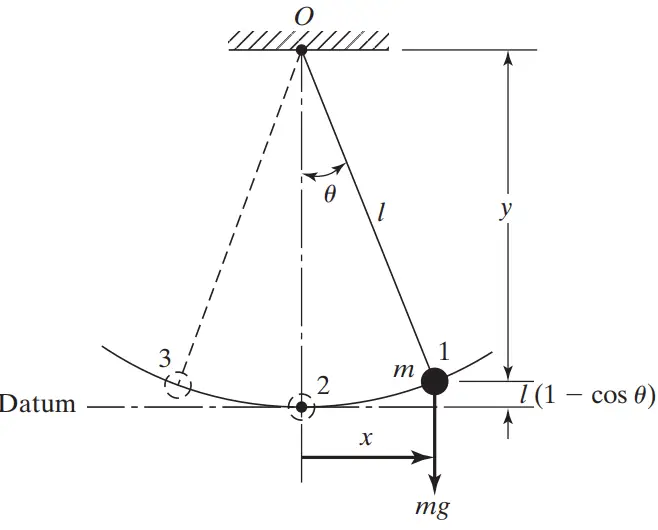
برای مثال، یک پاندول ساده (Simple Pendulum) را در نظر بگیرید. اگر جرم پاندول 𝑚 پس از جابجایی زاویه‌ای 𝜃 رها شود، در موقعیت ۱، سرعت و انرژی جنبشی پاندول صفر است. اما انرژی پتانسیل (Potential Energy) آن برابر با 𝐸𝑝=𝑚𝑔𝑙(۱−cos⁡𝜃) است. از آنجا که نیروی گرانش 𝑚𝑔 یک گشتاور 𝜏=𝑚𝑔𝑙sin⁡𝜃 ایجاد می‌کند، پاندول از موقعیت ۱ به سمت چپ نوسان می‌کند. این باعث شتاب زاویه‌ای در جهت عقربه‌های ساعت می‌شود و تمام انرژی پتانسیل به انرژی جنبشی (Kinetic Energy) تبدیل می‌شود. پاندول در موقعیت ۲ متوقف نمی‌شود و به سمت موقعیت ۳ ادامه نوسان می‌دهد. با این حال، وقتی از موقعیت ۲ عبور می‌کند، گرانش باعث کاهش سرعت پاندول می‌شود.

در موقعیت ۳، سرعت پاندول صفر می‌شود و تمام انرژی جنبشی به انرژی پتانسیل تبدیل می‌شود. سپس، پاندول به دلیل گرانش دوباره شتاب می‌گیرد و به نوسان به سمت راست ادامه می‌دهد. این فرآیند تکرار می‌شود و پاندول نوسان می‌کند. اما در عمل، دامنه نوسان 𝜃 به تدریج کاهش می‌یابد و پاندول به دلیل میرایی محیطی (Environmental Damping) در نهایت متوقف می‌شود. این به این معناست که مقداری انرژی در هر چرخه ارتعاش به دلیل وجود میرا کننده (Damping) از دست می‌رود.

دسته‌بندی ارتعاشات (Classification of Vibrations)

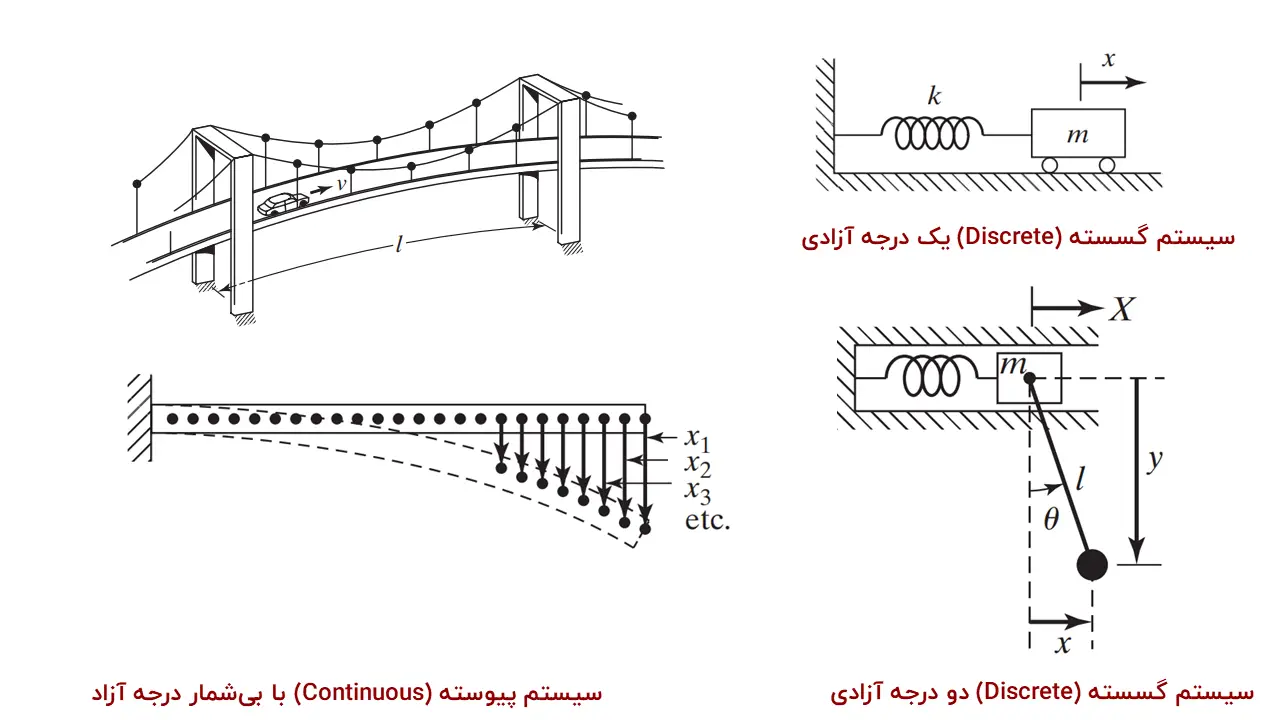
۱- سیستم‌های گسسته (Discrete) و سیستم‌های پیوسته (Continuous)

سیستم‌های ارتعاشات مکانیکی (Mechanical Vibrations) بر اساس درجات آزادی سیستم به دو دسته کلی تقسیم می‌شوند:

• سیستم‌های گسسته (Discrete Systems)
• سیستم‌های پیوسته (Continuous Systems)

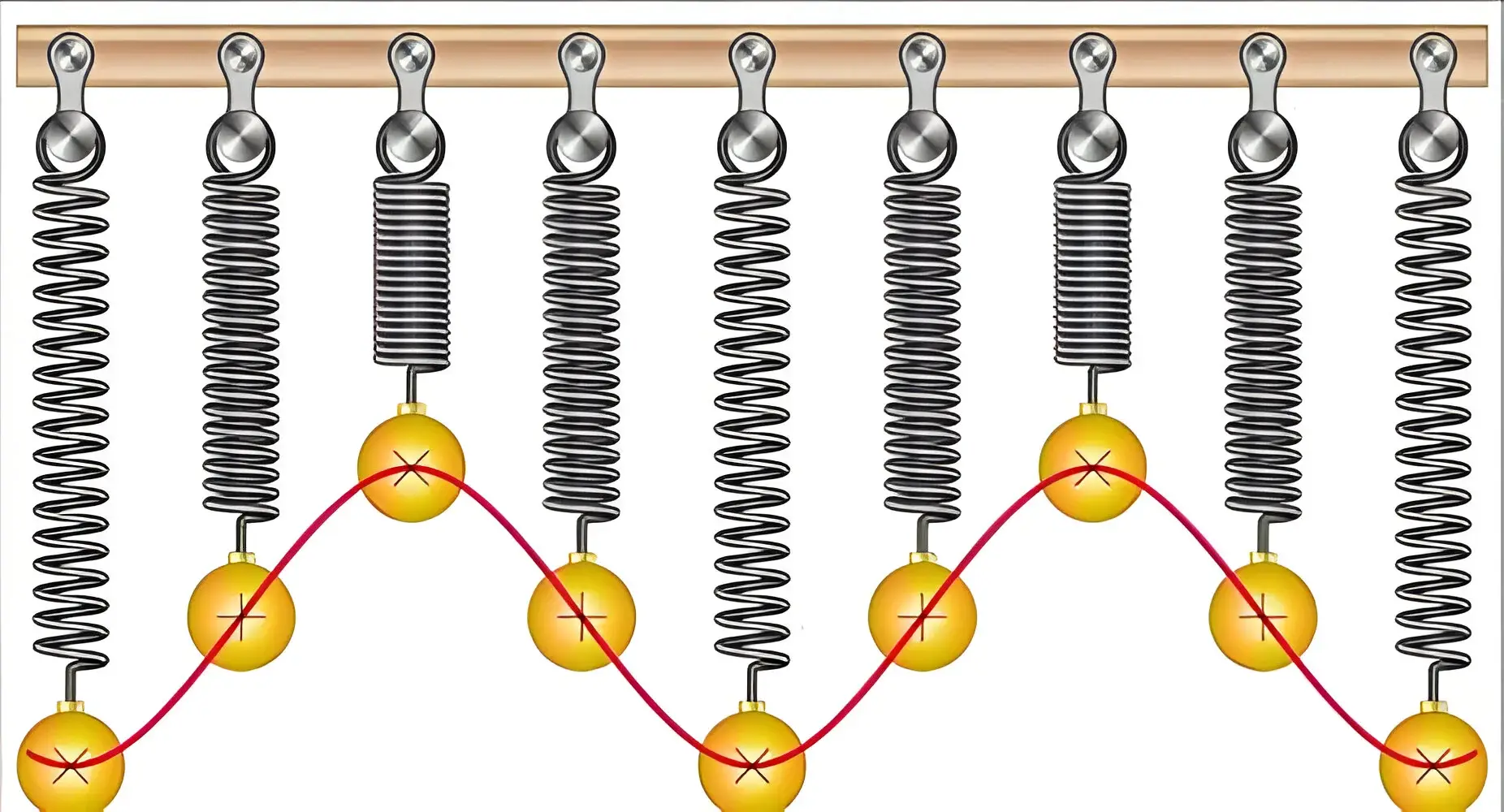
در سیستم‌های گسسته، تعداد محدودی درجه آزادی (Degrees of Freedom) وجود دارد. این سیستم‌ها شامل جرم‌هایی هستند که در نقاط خاصی قرار دارند و انرژی توسط فنرها و دمپرها بین این نقاط منتقل می‌شود. مثال‌هایی از سیستم‌های گسسته شامل سیستم‌های جرم-فنر (Mass-Spring Systems)، پاندول‌های ساده و سیستم‌های مکانیکی با چند جرم و فنر است. این سیستم‌ها با معادلات دیفرانسیل معمولی (ODE) مدل‌سازی می‌شوند و تعداد درجات آزادی آن‌ها به تعداد جرم‌ها و فنرهای موجود بستگی دارد.

در مقابل، سیستم‌های پیوسته دارای بی‌نهایت درجه آزادی هستند. در این سیستم‌ها، جرم و انرژی به صورت پیوسته در طول یک جسم توزیع می‌شود. مثال‌هایی از سیستم‌های پیوسته شامل تیرها، صفحات، شفت‌ها و پوسته‌ها هستند. این سیستم‌ها با معادلات دیفرانسیل جزئی (PDE) مدل‌سازی می‌شوند که رفتار دینامیکی سیستم را در طول زمان توصیف می‌کنند. حل این معادلات نیازمند روش‌های عددی پیچیده و کامپیوتری است.

در سیستم‌های گسسته، تحلیل مودال (Modal Analysis) و استفاده از ماتریس‌های جرم (Mass Matrices) و سختی (Stiffness Matrices) به ساده‌سازی تحلیل کمک می‌کنند. در سیستم‌های پیوسته، روش‌های تحلیلی مانند روش جداسازی متغیرها (Method of Separation of Variables) و روش‌های عددی مانند روش اجزای محدود (FEM) برای تحلیل ارتعاشات استفاده می‌شوند.

به طور خلاصه، تفاوت اصلی بین سیستم‌های گسسته و پیوسته در نحوه توزیع جرم و انرژی و تعداد درجات آزادی آن‌هاست که روش‌های مدل‌سازی و تحلیل متفاوتی را می‌طلبد.

۲- ارتعاشات آزاد (Free)، اجباری (Forced) و ارتعاشات خود تحریک (Self-excited)

ارتعاشات مکانیکی با توجه به عامل ارتعاشات به سه دسته کلی تقسیم می‌شوند:

• ارتعاشات آزاد (Free Vibrations)
• ارتعاشات اجباری (Forced Vibrations)
• ارتعاشات خود تحریک (Self-excited Vibrations)

ارتعاشات آزاد (Free Vibrations) زمانی رخ می‌دهد که یک سیستم بدون تأثیر نیروی خارجی (External Force) در حال نوسان باشد. در این حالت، سیستم پس از یک تغییر وضعیت اولیه، به دلیل انرژی ذخیره شده در آن شروع به نوسان می‌کند و به تدریج به دلیل میرایی و مقاومت محیطی، انرژی خود را از دست می‌دهد تا زمانی که به حالت تعادل برسد. مثال‌هایی از ارتعاشات آزاد شامل نوسان یک پاندول ساده و سیستم جرم-فنر است.

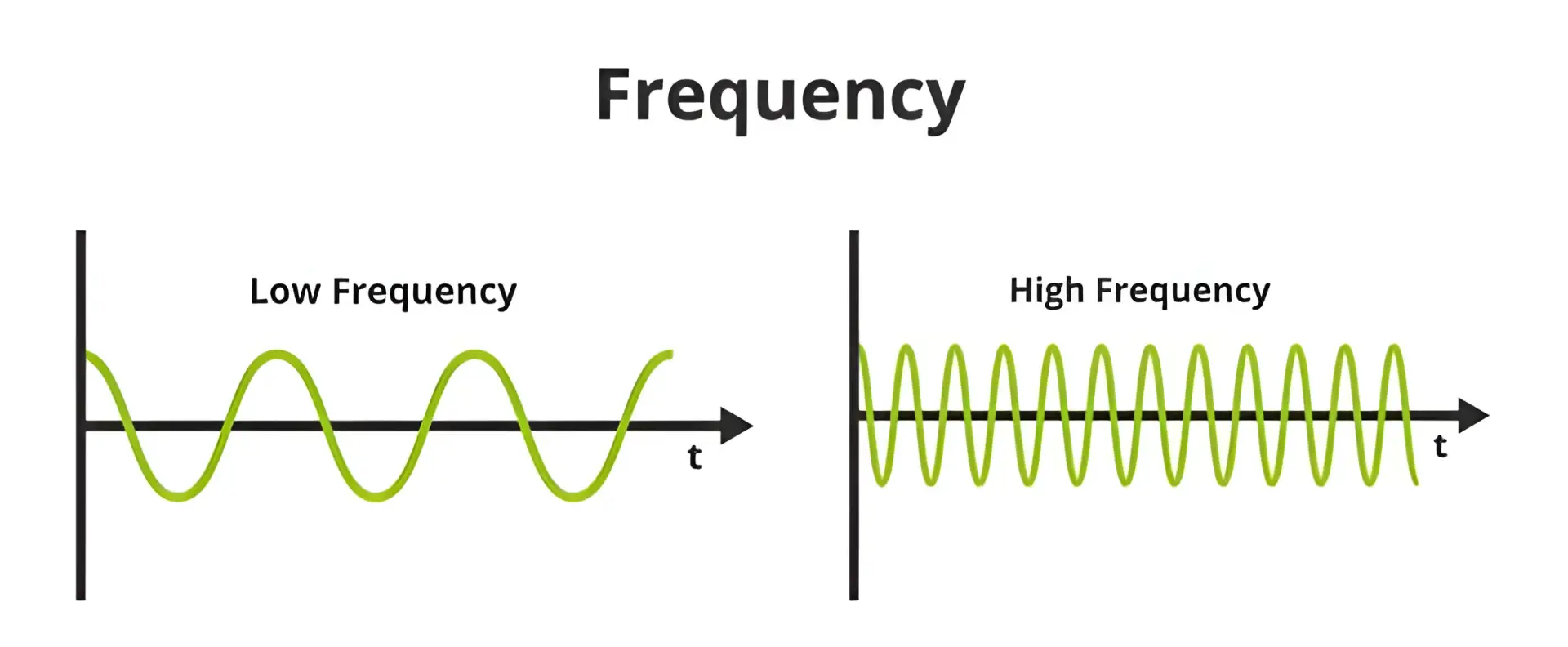
فرکانس ارتعاشات آزاد به خواص فیزیکی سیستم مانند جرم، سختی و میرایی ساختاری آن بستگی دارد و به عنوان فرکانس طبیعی (Natural Frequency) سیستم شناخته می‌شود.

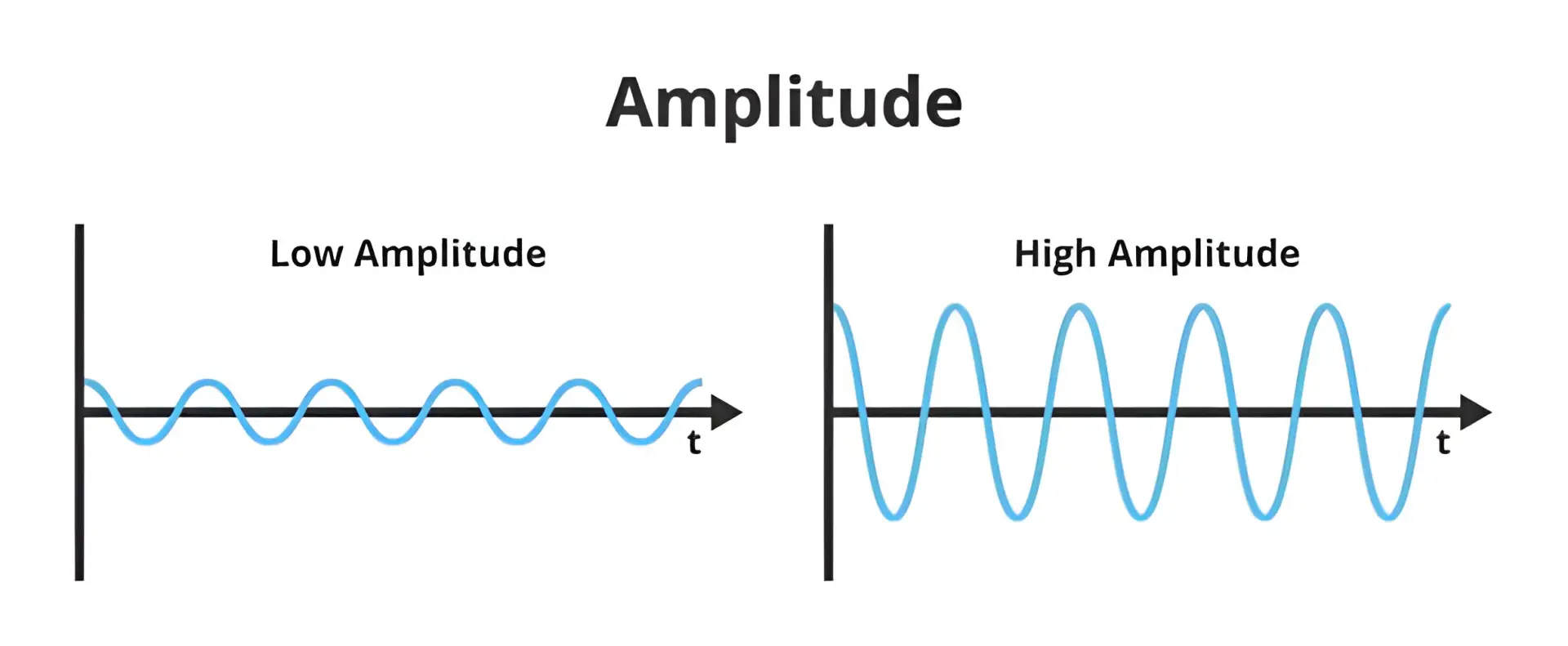
در حالیکه دامنه ارتعاشات مکانیکی یک سیستم، متناسب با اختلاف انرژی وضعیت اولیه سیستم نسبت به وضعیت تعادلش است.

در مقابل، ارتعاشات اجباری (Forced Vibrations) زمانی رخ می‌دهد که یک سیستم تحت تأثیر نیروی خارجی (External Force) قرار گیرد. این نیروی خارجی می‌تواند متناوب یا غیر متناوب باشد. در این حالت، سیستم با فرکانس نیروی خارجی نوسان می‌کند. اگر فرکانس نیروی خارجی با فرکانس طبیعی سیستم برابر باشد، پدیده‌ ی تشدید (Resonance Phenomenon) رخ می‌دهد که می‌تواند منجر به افزایش شدید دامنه نوسانات و در نهایت خرابی سیستم شود. مثال‌هایی از ارتعاشات اجباری شامل ارتعاشات ناشی از موتورهای نامتعادل (Unbalanced Engines)، نیروهای باد بر روی پل‌ها و ارتعاشات ایجاد شده توسط ماشین‌آلات صنعتی می‌باشد.

در نتیجه در ارتعاشات آزاد، سیستم به دلیل انرژی ذخیره شده خود نوسان می‌کند، در حالی که در ارتعاشات اجباری، سیستم تحت تأثیر نیروی خارجی نوسان می‌کند. بررسی و تحلیل هر دو نوع ارتعاش برای طراحی و ایمنی سیستم‌های مکانیکی اهمیت زیادی دارد.

در ارتعاشات خود تحریک (Self-excited Vibrations)، ارتعاشات در اثر برهم‌ کنش اجزای داخلی سیستم ارتعاشاتی بوجود می‌آید. ارتعاشات در این سیستم‌ها به‌طور خود به خود (Spontaneously) رخ می‌دهد و در ادامه دامنه ارتعاشات افزایش می‌یابد تا زمانی که اثرات غیرخطی این افزایش دامنه را محدود کند.

در ارتعاش خود تحریک نیروی متناوب که نوشان را ایجاد و حفظ می‌کند توسط حرکت اجزای سیستم ایجاد و کنترل می‌شود. هنگامی که حرکت متوقف شود، نیروی متناوب نیز ناپدید می‌شود. در حالیکه در یک ارتعاش اجباری، عامل ارتعاشات (نیروی متناوب) مستقل از سیستم و حرکت آن است و زمانی که حرکت ارتعاشی متوقف می‌شود نیز باقی می‌ماند.

وقوع ارتعاش خود تحریک در یک سیستم فیزیکی ارتباط نزدیکی با پایداری وضعیت‌های تعادلی سیستم دارد. اگر سیستم از موقعیت تعادل بهم بخورد، عموماً نیروهایی ظاهر می‌شوند که باعث می شوند سیستم به سمت موقعیت تعادل حرکت کند یا از آن دور شود. در مورد دوم موقعیت تعادل ناپایدار است. سپس سیستم ممکن است با افزایش دامنه نوسان کند یا به طور یکنواخت از موقعیت تعادل عقب نشینی کند تا زمانی که محدودیت های غیرخطی یا محدود کننده ظاهر شوند. در صورتی که سیستم مختل به حالت نوسانی میرا یا مجانبی به موقعیت تعادل نزدیک شود، وضعیت تعادل پایدار است.

۳- ارتعاشات بدون میرا کننده (Undamped) و با میرا کننده (Damped)

ارتعاشات بدون میرا کننده زمانی رخ می‌دهد که هیچ مقاومتی برای کاهش انرژی ارتعاشی سیستم وجود نداشته باشد. در این حالت، سیستم به نوسان خود ادامه می‌دهد و انرژی ارتعاشی به طور دائمی بین انرژی پتانسیل و انرژی جنبشی تبدیل می‌شود. برای مثال، یک پاندول ساده در خلا که هیچ مقاومتی در برابر حرکت آن وجود ندارد، به طور مداوم نوسان خواهد کرد. فرکانس و دامنه این نوع ارتعاشات به خواص فیزیکی سیستم، مانند جرم و سختی، بستگی دارد.

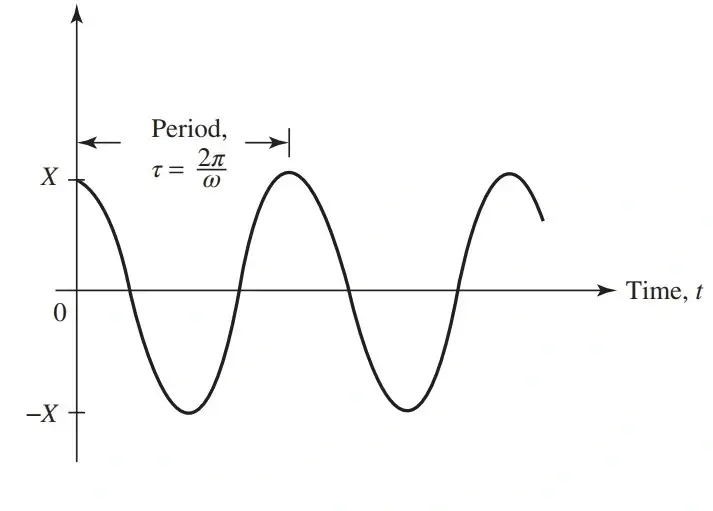
در مقابل، ارتعاشات با میرا کننده زمانی رخ می‌دهد که مقاومتی برای کاهش انرژی ارتعاشی سیستم وجود داشته باشد. این مقاومت می‌تواند از طریق عوامل مختلفی مانند اصطکاک (Friction)، مقاومت هوا (Air Resistance) یا استفاده از میرا کننده‌ها ایجاد شود. در این حالت، انرژی ارتعاشی به تدریج کاهش می‌یابد و سیستم به آرامی به حالت تعادل می‌رسد. مثال‌هایی از ارتعاشات با میرا کننده شامل نوسان یک پاندول در هوا و سیستم‌های جرم-فنر با میرا کننده هستند. مقدار میرایی موجود در سیستم می‌تواند تاثیر زیادی بر رفتار ارتعاشی آن داشته باشد و به سه دسته زیر بحرانی, بحرانی و فوق بحرانی تقسیم می‌شود.

در حالت زیر بحرانی (Under-Damped)، سیستم همچنان نوسان می‌کند اما دامنه نوسانات به تدریج کاهش می‌یابد. در حالت بحرانی (Critically Damped)، سیستم بدون نوسان به حالت تعادل بازمی‌گردد و در حالت فوق بحرانی (Over-Damped)، سیستم با سرعت کمتری نسبت به حالت بحران به حالت تعادل باز می‌گردد.

بنابراین، ارتعاشات بدون میرا کننده بدون هیچ مقاومتی ادامه می‌یابند، در حالی که ارتعاشات با میرا کننده به تدریج انرژی خود را از دست می‌دهند و به حالت تعادل می‌رسند. بررسی و تحلیل میرایی در سیستم‌های مکانیکی برای پیش‌بینی رفتار ارتعاشی و طراحی بهینه اهمیت دارد.

۴- ارتعاشات خطی و غیرخطی (Linear and Nonlinear Vibrations)

ارتعاشات خطی و غیرخطی دو مفهوم اساسی در تحلیل سیستم‌های ارتعاشی هستند. ارتعاشات خطی (Linear Vibrations) زمانی رخ می‌دهند که اجزای اصلی یک سیستم ارتعاشی، مانند فنر، جرم و دمپر، به صورت خطی رفتار کنند. در این حالت، معادلات دیفرانسیلی که رفتار سیستم را توصیف می‌کنند، خطی هستند و اصل برهم‌نهی معتبر است.

در مقابل، ارتعاشات غیرخطی (Nonlinear Vibrations) زمانی رخ می‌دهند که یکی یا بیشتر از اجزای اصلی سیستم به صورت غیرخطی رفتار کنند. در این موارد، معادلات دیفرانسیلی که رفتار سیستم را توصیف می‌کنند، غیرخطی هستند و اصل برهم‌نهی معتبر نیست. این امر تحلیل و بررسی سیستم‌های غیرخطی را پیچیده‌تر می‌کند و نیاز به تکنیک‌های تحلیلی پیشرفته‌تر دارد. سیستم‌های ارتعاشی با افزایش دامنه نوسانات تمایل به رفتار غیرخطی پیدا می‌کنند، به همین دلیل تحلیل ارتعاشات غیرخطی برای سیستم‌های ارتعاشی در دنیای واقعی، عملی ضروری است.

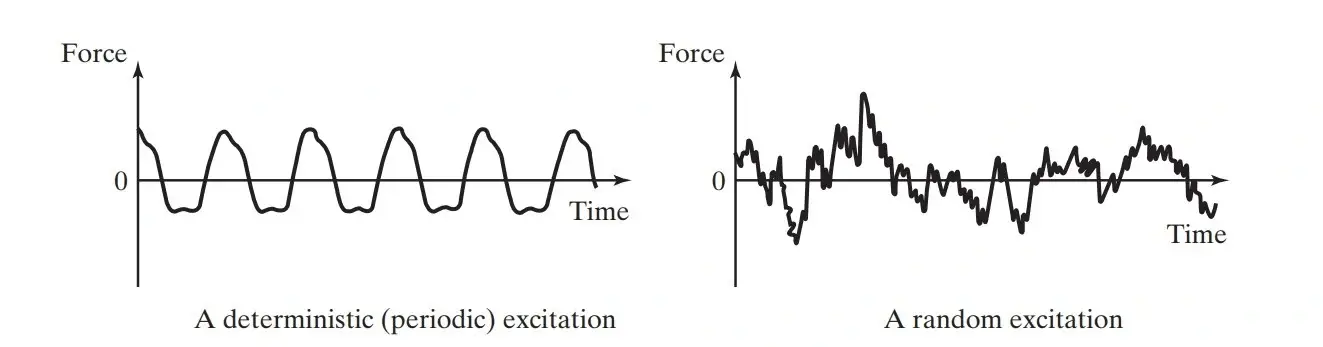
۵- ارتعاشات معین و تصادفی (Deterministic and Random Vibrations)

ارتعاشات معین و تصادفی دو نوع اصلی از ارتعاشات هستند که هرکدام ویژگی‌ها و کاربردهای خاص خود را دارند. ارتعاشات معین (Deterministic Vibrations) زمانی رخ می‌دهند که مقدار یا اندازه تحریک (نیرو یا حرکت) که بر سیستم ارتعاشی اثر می‌گذارد، در هر لحظه از زمان مشخص باشد. در این حالت، ارتعاشات ایجاد شده نیز معین و قابل پیش‌بینی‌ هستند. این نوع ارتعاشات را می‌توان با استفاده از مدل‌های ریاضی و تحلیل‌های دقیق بررسی کرد.

در مقابل، ارتعاشات تصادفی (Random Vibrations) زمانی رخ می‌دهند که مقدار تحریک در هر لحظه از زمان قابل پیش‌بینی نباشد و به صورت تصادفی تغییر کند. این نوع تحریک‌ها ممکن است ناشی از عواملی مانند سرعت باد (Wind Speed)، ناهمواری جاده (Road Irregularities)، یا حرکت زمین در طول زمین‌لرزه (Earthquake) باشد. ارتعاشات ایجاد شده در این شرایط نیز تصادفی و غیرقابل پیش‌بینی هستند و تنها می‌توان آن‌ها را با استفاده از مقادیر آماری مانند میانگین (Mean) و واریانس (Variance) توصیف کرد.

در ارتعاشات تصادفی، جمع‌آوری و تحلیل تعداد زیادی از داده های تحریک‌ می‌تواند الگوهای آماری مشخصی را نشان دهد. به عنوان مثال، می‌توان میانگین و مقدار میانگین مربعی تحریک‌ها را تخمین زد. تحلیل این نوع ارتعاشات نیازمند استفاده از روش‌های آماری و تکنیک‌های تحلیل سیگنال (Signal Analysis Techniques) است.

نمودارهای مقایسه‌ای بین تحریک‌های معین و تصادفی نشان می‌دهند که چگونه رفتار سیستم‌های ارتعاشی در برابر این دو نوع تحریک متفاوت است. در سیستم‌های معین، پاسخ سیستم نیز معین است و به صورت دقیق قابل پیش‌بینی است. اما در سیستم‌های تصادفی، پاسخ سیستم نیز تصادفی بوده و تنها می‌توان آن را با استفاده از توابع آماری و تحلیل‌های پیچیده‌تر توصیف کرد.

دانش در مورد این دو نوع ارتعاش و تفاوت‌های آن‌ها برای مهندسان و محققان اهمیت بسیاری دارد تا بتوانند رفتار سیستم‌های مختلف را در شرایط مختلف پیش‌بینی و تحلیل کنند و از این طریق طراحی‌های بهتری انجام دهند.

پدیده‌های مهم سیستم‌های ارتعاشی

پدیده تشدید (Resonance Phenomenon)

یکی از مهم‌ترین مسائل در مطالعه ارتعاشات، پدیده تشدید است. زمانی که فرکانس طبیعی (Natural Frequency) ارتعاش یک ماشین یا سازه با فرکانس تحریک خارجی (External Excitation Frequency) همزمان شود، تشدید رخ می‌دهد که می‌تواند منجر به تغییر شکل‌های بیش از حد و خرابی شود. به عنوان مثال، پل Tacoma Narrows به دلیل ناپایداری آیرودینامیکی و تشدید، فروپاشید. به دلیل این اثرات ویرانگر، تحلیل ارتعاشات به یک روش استاندارد در طراحی و توسعه بسیاری از سیستم‌های مهندسی تبدیل شده است.

پدیده ی فلاتر (Flutter Phenomenon)

پدیده فلاتر به عنوان یک ناپایداری دینامیکی (Dynamic Instability) شناخته می‌شود که در سازه‌های الاستیک (Elastic Structures) در تعامل با جریان سیال (Fluid Flow) رخ می‌دهد. این پدیده شامل ارتعاشات شدید سازه با دامنه‌های به سرعت افزایش‌یابنده است که معمولاً منجر به آسیب جدی یا تخریب کامل سازه می‌شود. فلاتر زمانی رخ می‌دهد که پارامترهای تعامل سازه-سیال (Structure-Fluid Interaction Parameters) به مقادیر بحرانی خاصی برسند و انرژی جریان به سرعت توسط سازه جذب و به انرژی ارتعاشات مکانیکی تبدیل شود. در مهندسی، برای جلوگیری از فلاتر باید طراحی مناسب سازه‌ها انجام شود یا مکانیزم‌های کنترلی جهت سرکوب ارتعاشات تعبیه گردد.

مراحل تحلیل یک سیستم ارتعاشی (Analyzing a Vibratory System)

مرحله اول: مدل‌سازی ریاضی (Mathematical Modeling)

مدل‌سازی ریاضی اولین و اساسی‌ترین مرحله در تحلیل ارتعاشات است. هدف از این مرحله، ارائه یک مدل ریاضی از سیستم است که تمام ویژگی های اصلی سیستم را در بر میگیرد. مدل ریاضی باید جزئیات کافی را در بر داشته باشد تا بتوان سیستم را از طریق معادلات, بدون اینکه بیش از حد پیچیده شود, توصیف کرد. مدل ریاضی می‌تواند بسته به رفتار سیستم خطی یا غیرخطی باشد. مدل‌های خطی امکان حل سریع و ساده را فراهم می‌کنند، اما گاهی اوقات مدل‌های غیرخطی ویژگی‌هایی از سیستم را نشان می‌دهند که با مدل‌های خطی قابل پیش‌بینی نیستند.

مرحله دوم: استخراج معادلات حاکم (Deriving Governing Equations)

پس از مدل‌سازی ریاضی، مرحله بعدی استخراج معادلات حاکم است. این معادلات معمولاً به صورت معادلات دیفرانسیل ارائه می‌شوند که رفتار دینامیکی سیستم را تحت شرایط ورودی مشخص توصیف می‌کنند. این معادلات بر اساس اصول فیزیکی مانند قانون دوم نیوتن، اصول انرژی و ممان اینرسی استخراج می‌شوند. در سیستم‌های پیچیده‌تر، ممکن است نیاز به استفاده از روش‌های عددی برای استخراج معادلات حاکم باشد.

مرحله سوم: حل معادلات (Solving the Equations)

پس از استخراج معادلات حاکم، مرحله بعدی حل این معادلات است. برای سیستم‌های خطی، معادلات دیفرانسیل به راحتی قابل حل هستند و می‌توان پاسخ‌های تحلیلی دقیقی بدست آورد. اما برای سیستم‌های غیرخطی، ممکن است نیاز به استفاده از روش‌های عددی مانند روش رانج کوتا (Runge–Kutta)، روش المان محدود و یا شبیه‌سازی‌های کامپیوتری باشد. هدف از حل معادلات، بدست آوردن پاسخ زمانی سیستم تحت شرایط اولیه و تحریکات خارجی مشخص است.

مرحله چهارم: تفسیر نتایج (Interpreting the Results)

مرحله نهایی در تحلیل ارتعاشات، تفسیر نتایج است. نتایج بدست آمده از حل معادلات باید تحلیل و تفسیر شوند تا بتوان رفتار سیستم را تحت شرایط مختلف درک کرد. این مرحله شامل بررسی پایداری، پاسخ فرکانسی، و تاثیرات عوامل مختلف بر سیستم است. همچنین ممکن است نیاز به بررسی نتایج با داده‌های تجربی باشد تا صحت و دقت مدل و تحلیل تایید شود.

منابع:

Dukkipati, V. Rao, and Jay Srinivas. Textbook of Mechanical Vibrations. PHI Learning Pvt. Ltd., 2012.
Rao, Singiresu S. “Mechanical Vibrations, in SI Units, Global Edition.” ed: Pearson, London (2017).
Wikipedia
Britannica
Harvard Math
www.newscientist.com
slideplayer.com