روش اجزاء (المان) محدود (FEM)

روش اجزاء (المان) محدود (FEM) چیست؟

روش اجزاء محدود (Finite Element Method=FEM) یا روش المان محدود (Finite Element Method=FEM) معمولا روشی است عددی، برای حل معادلات دیفرانسیل معمولی (Ordinary Differential Equation=ODE) و معادلات دیفرانسیل با مشتقات جزئی (Partial Differential Equation=PDE). معادلات حاکم بر اغلب مسائل مهندسی معادلات دیفرانسیل هستند. بنابراین با استفاده از روش اجزاء محدود (FEM) می‌توان طیف وسیعی از مسائل مهندسی پیچیده را حل کرد.

توصیه مکادمی؛ روش اجزاء محدود کاربردی (کلاس‌های اجزاء محدود کارشناسی مهندسی مکانیک دانشگاه تهران)

چرا روش اجزاء (المان) محدود (FEM) روشی معمولا عددی است؟

اساس روش اجزاء محدود شامل مراحل زیر است:

1. گسسته‌سازی هندسه (Discretization)
2. در نظر گرفتن تابعی برای فرم کلی پاسخ در هر المان بر حسب مقادیر گره‌ای (Interpolation Function or Shape Function)
3. محاسبه ماتریس‌های مشخصه (ماتریس اینرسی خطی (جرم)، ماتریس اینرسی دورانی، ماتریس دمپینگ (میرائی) و ماتریس سفتی) برای هر المان (Element Characteristics Matrix)
4. مونتاژ المان‌ها برای ساخت ماتریس‌های مشخصه کل سازه (Assemblage)
5. اعمال شرایط مرزی به دستگاه معادلات ماتریسی (Apply Boundary Conditions)
6. اعمال شرایط اولیه در مسائل دینامیک (Apply Initial Conditions)
7. حل دستگاه معادلات جبری (در مسائل استاتیک) یا حل دستگاه معادلات دیفرانسیل معمولی (در مسائل دینامیک)

بنابراین مادامی که در مراحل ۳ام و ۷ام از روش‌های عددی استفاده نشود، روش اجزاء محدود (به دلیل در نظر گرفتن فرم کلی پاسخ یعنی مرحله ۲) روشی تحلیلی با تقریب (Analytical Approximate Solution) است. در عمل مسائل محدودی همانند مدل سازی سازه با استفاده از المان‌های خرپا (Truss)، تیر (Beam) و فریم (Frame) را می‌توان با روش اجزاء محدود به صورت تحلیلی حل کرد.

چرا از روش اجزاء (المان) محدود (FEM) استفاده می‌کنیم؟

به طور بسیار خلاصه، در مسائلی با هندسه، رفتار ماده، بارگذاری و شرایط مرزی پیچیده ناچار به استفاده از روش اجزاء محدود هستیم. برای درک بهتر این موضوع روش‌های مختلف حل مسئله به طور خلاصه آورده شده است.

برای حل مسائل سه دسته روش وجود دارد:

1. روش‌های تحلیلی (Analytical Methods)
2. روش‌های نیمه تحلیلی (Semi-analytical Methods)
3. روش‌های عددی (Numerical Methods)

روش‌های تحلیلی (Analytical Methods)

روش‌های تحلیلی (Analytical Methods) دقیق و بسیار کم هزینه هستند، اما صرفا توانایی حل مسائل محدودی آن هم معمولا با در نظر گرفتن فرضیات ساده کننده را دارند. با پیچیده شدن هندسه مسئله، رفتار ماده و شرایط مرزی، این روش‌ها با بن‌بست مواجه خواهند شد.

روش‌های تحلیلی را می‌توان به حل دقیق (Exact Solution) و حل تقریبی (Approximate Solution) تقسیم بندی نمود. از میان روش‌های تقریبی (Approximate Methods) که در روش اجزاء محدود بکار گرفته می‌شود، می‌توان به روش گسسته سازی با سری (Series Discretization Method) که در استخراج توابع شکل (Shape Functions) بکار گرفته می‌شود و روش Lumped Parameters که در استخراج ماتریس اینرسی به روش Lumped Mass بکار گرفته می‌شود.

اغلب روش‌هایی که در ریاضیات عمومی، معادلات دیفرانسیل و ریاضی مهندسی فرا آموخته‌اید، روش‌هایی تحلیلی هستند.

روش‌های نیمه تحلیلی (Semi-analytical Methods)

این روش‌ها نسبت به روش‌های تحلیلی محدودیت کمتری دارند اما توانایی حل تمامی مسائل پیچیده را ندارد. روش‌های نیمه تحلیلی (Semi-analytical Methods) مشابه روش‌های تحلیلی هستند با این تفاوت که حل مسئله را با روش‌های تحلیلی پیش‌ می‌برند و زمانی که این روش‌ها با محدودیت مواجه شدند، تقریب یا روش‌های عددی وارد مسئله می‌شوند.

روش‌های عددی (Numerical Methods)

هرچند که روش‌های عددی (Numerical Methods) قدرتمندترین روش برای حل مسائل پیچیده و دشوار هستند، اما هزینه محاسبه بالایی را دارند. روش‌های عددی تنوع بسیار بالایی دارند، بنابراین صرفا تعدادی از این روش‌ها که اغلب دانشجویان با آن‌ها آشنا هستند را لیست کرده‌ایم.

• مشتق گیری عددی (Numerical Differentiation)
• انتگرال گیری عددی (Numerical Integration)
• روش تفاضل محدود (Finite Difference Method)
• روش اجزاء محدود (Finite Element Method)
• روش حجم محدود (Finite Volume Method)

بنابراین از آنجایی که روش‌های تحلیلی (Analytical Methods) و روش‌های نیمه تحلیلی (Semi-analytical Methods) قادر به حل مسائلی با هندسه، ماده و شرایط مرزی پیچیده نیستند، به روش‌های عددی روی می‌آوریم. از میان روش‌های عددی بیان شده روش اجزاء محدود (Finite Element Method) روشی بسیار قدرتمند برای حل مسائل مکانیک جامدات (Solid Mechanics)، انتقال حرارت (Heat Transfer)، الکترومغناطیس (Electromagnetic) و حتی مکانیک سیالات (Fluid Mechanics) است.

مراحل روش اجزاء (المان) محدود (FEM)

روش اجزاء محدود بر اساس گسسته‌سازی هندسه مسئله به ناحیه‌هایی کوچک به نام المان (Element)، استوار است. سپس فرم کلی پاسخ متغیر میدانی (Field Variable) در هر المان بر حسب مقادیر گره‌ای (Nodal Variables) درون‌یابی (Interpolation) می‌شود. برای مثال متغیر میدانی بسیاری از مسائل مکانیک جامدات، میدان جابجایی {U} است. مقادیر گره‌ای با {a} و ماتریس توابع شکل (Shape Function) با [N] نشان داده شده است.

{U(x,y,x,t)}=[N(x,y,z)]{a(t)}

در ادامه با استفاده از یکی از رویکردهای موجود (Direct Approach, Variational Approach, Weighted Residual Approach)، معادلات ماترسی حاکم بر رفتار المان استخراج می‌شود. برای مثال، این معادلات در مسائل استاتیک سازه‌ای (Structural) شامل ماتریس سفتی (Stiffness Matrix) و بردار نیرو (Force Vector) است.

سپس ماتریس سفتی و بردار نیروی تک تک المان‌ها مونتاژ می‌شود تا دستگاه معادلات حاکم بر کل هندسه مسئله حاصل شود. در گام بعدی، شرایط مرزی و در صورت نیاز (در مسائل دینامیک) شرایط اولیه نیز اعمال می‌شود.

بنابراین در مسائل استاتیک دستگاه معادلات جبری حل می‌شود و در مسائل دینامیک، دستگاه معادلات دیفرانسیل معمولی از نوع مسئله مقدار اولیه (Initail Value Problem) با استفاده از تکینیک‌های انتگرال‌گیری عددی حل می‌شوند.

۱- گسسته‌سازی هندسه (Discretization)

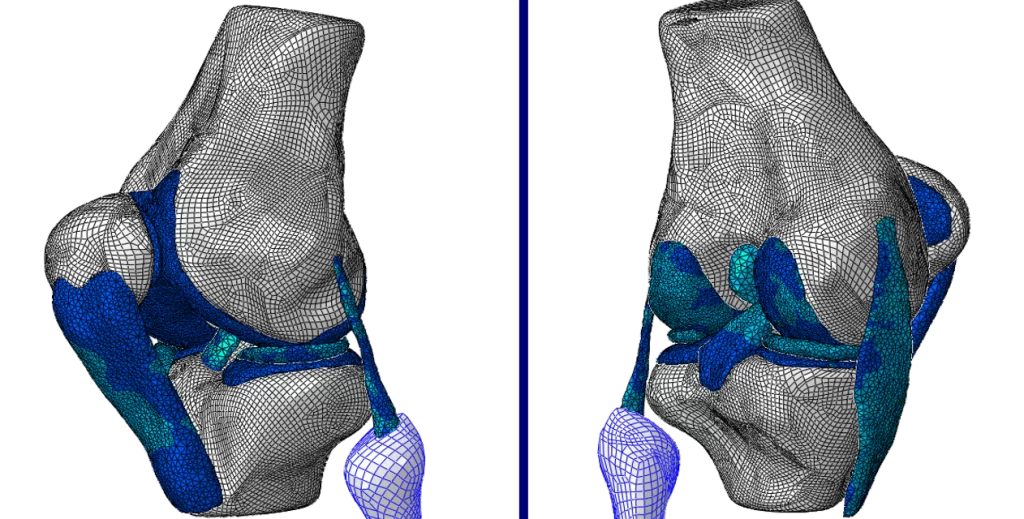
ابتکار روش اجزاء محدود، گسسته‌سازی هندسه اصلی مسئله (که در بیشتر موارد هندسه‌ای پیچیده است) به اجزایی کوچک به نام المان است. المان ها در گوشه‌های خود توسط گره‌ها (Nodes) به هم متصل شده‌اند. تبدیل هندسه پیوسته مسئله به مجموعه‌ای المان‌ها و گره‌ها را مش‌بندی (Meshing) می‌گویند.

۲- در نظر گرفتن فرم کلی پاسخ در هر المان بر حسب مقادیر گره‌ای (Interpolation Function or Shape Function)

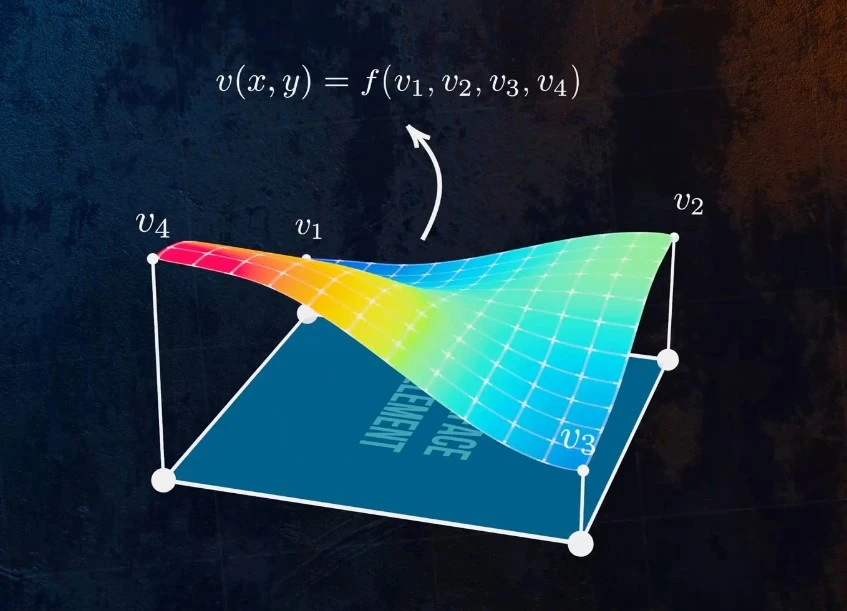
خب پس از گسسته‌سازی هندسه مسئله، حال نوبت به Interpolation می‌رسد. از آنجایی که در حالت کلی (هندسه، بار و شرایط مرزی پیچیده) پاسخ تحلیلی و دقیق موجود در هر المان را نیز نمی‌توان محاسبه کرد به استفاده از روش‌های تحلیلی و تقریبی روی می‌آوریم. در نخستین گام باید فرم کلی پاسخ در هر المان را بر حسب مقادیر گره‌ای درون یابی کنیم. سپس با نوشتن متغیر میدانی (مثلا u(x,y,z)) به صورت حاصل ضرب توابع شکل در مقادیر گره‌ای روند حل مسئله را ادامه می‌دهیم.

{U(x,y,x,t)}=[N(x,y,z)]{a(t)}

۳- محاسبه ماتریس‌های مشخصه برای هر المان (Element Characteristics Matrix)

برای محاسبه ماتریس‌های مشخصه (ماتریس اینرسی، ماتریس دمپینگ، ماتریس سفتی، بردار نیرو) هر المان سه رویکرد وجود دارد:

رویکرد مستقیم (Direct Approach)

رویکرد مستقیم (Direct Approach) همان بکاگیری روابط تعادل (Balance Law) مانند معادله پیوستگی جرم (Continuity)، معادله ممنتوم خطی (Linear Momentum)، معادله ممنتوم زاویه‌ای (Angular Momentum) و معادله انرژی است.

در بیشتر مسائل مکانیک جامدات مانند مسئله خرپا، تیر، فریم و … معادله بالانس ممنتوم خطی (Linear Momentum) یا همان قانون دوم نیوتن کافی است.

رویکرد حساب تغییرات (Variational Approach)

این روش بر مبنای اکسترمم کردن فانکشنال (Functional) حاکم بر مسئله است. که با اعمال وریشن (Variation) حاصل می‌شود. این روش مختص مسائلی است که دارای فانکشنال باشند و بتوان مسئله را به صورت variation فرموله کرد. در مسائل مکانیک جامدات، لاگرانژین سیستم همان فانکشنال حاکم بر مسئله است.

رویکرد باقی‌مانده وزنی (Weighted Residual Approach)

این روش بر مبنای به کارگیری معادلات دیفرانسل حاکم بر مسئله است و جامع‌­ترین روش برای حل مسائل المان محدود است و نیازی به استخراج فانکشنال (Functional) حاکم بر مسئله و فرموله کردن مسئله به صورت variational نیست.

۴- مونتاژ المان‌ها برای ساخت ماتریس‌های مشخصه کل سازه (Assemblage)

پس از حصول دستگاه معادلات (جبری/دیفرانسیل) حاکم بر هر المان، باید تمامی المان به نحوی مونتاژ شوند که دستگاه معادلات (جبری/دیفرانسیل) حاکم بر کل سیستم بدست آید. فرآیند مونتاژ ماتریس‌های اینرسی، دمپینگ و سفتی هر المان بدین ترتیب است که سفتی هر المان به ماتریس‌های Global تبدیل شده سپس تمامی این ماتریس‌ها با یکدیگر جمع شده تا ماتریس‌های اینرسی، دمپینگ و سفتی کل سیستم حاصل گردد.

۵- اعمال شرایط مرزی به دستگاه معادلات (Apply Boundary Conditions)

دستگاه معادلات استخراج شده Singular است و باید شرایط مرزی حاکم بر مسئله وارد شود تا معادلات قابل حل شود.

۶- اعمال شرایط اولیه در مسائل دینامیک (Apply Initial Conditions)

در صورتی حل مسائل دینامیک با روش اجزاء محدود لازم است که علاوه بر شرایط مرزی، شرایط اولیه حاکم بر مسئله نیز اعمال گردند.

۷- حل دستگاه معادلات جبری (در مسائل استاتیک) یا حل دستگاه معادلات دیفرانسیل معمولی (در مسائل دینامیک)

با توجه به نوع معادلات حاکم بر مسئله، معادله جبری (مسائل استاتیک) و یا معادلات دیفرانسیل (مسائل دینامیک) و در نظر گرفتن خطی و یا غیرخطی بودن مسئله روش حل متفاوت خواهد بود. از طرفی دیگر در مسائل ارتعاشات، دو روش حل مستقیم معادلات و یا استفاده از روش آنالیز مودال وجود دارد.
روش نیوتن رافسون (Newton—Raphson) یکی از روش‌های کارآمد برای حل معادلات جبری غیرخطی است و روش‌های انتگرال گیری عددی Runge-Kutta و Newmark-β method برای حل معادلات دیفرانسل معمولی (ODE) مناسب است.

فهم روش اجزاء (المان) محدود (FEM)؛ تهیه شده توسط The Efficient Engineer

توصیه می‌کنم حتما تماشا کنید.

توصیه مکانیک‌آل؛ تماشا تمامی آموزش‌های The Efficient Engineer

نرم افزارهای روش اجزاء (المان) محدود (FEM)

با توجه به پیشرفت روز افزون علم مهندسی و کاربردهای مختلف آن، نیاز به ابزارهای طراحی بیش از پیش احساس می‌شود. مهندسان در صنایع مختلف قبل از تولید محصول نهایی، به کمک نرم‌افزارهای طراحی و شبیه سازی از عملکرد محصول خود اطمینان حاصل می‌کنند. این شبیه سازی‌ها علاوه بر کاهش هزینه‌های مربوط به آزمایش، به طراحان در راستای بهینه سازی و بهبود محصولات کمک می‌کنند.

نرم افزار آباکوس Abaqus

نرم افزار شبیه‌ساز آباکوس محصول شرکت Dassault Systems Simulia Corp بوده که در قبل به نام Abaqus Inc نیز شناخته می‌شده است. حلگر این نرم‌افزار برای اولین بار در سال ۱۹۷۸ توسط ۳ نفر از محققان دانشگاهی ساخته شد و سپس در سال ۱۹۹۲ نسخه کاملی از آن به طور رسمی منتشر شد تا در زمینه طراحی به کمک کامپیوتر ابزاری قدرتمند در اختیار مهندسان قرار دهد. از زمان انتشار آباکوس تا به امروز، محققان و مهندسان از آن در راستای شبیه‌سازی المان محدود و بهینه سازی طراحی‌های خود استفاده‌های بسیاری برده اند و هر ساله با منتشر شدن نسخه‌های جدیدتر آن، قابلیت‌های بیشتری به آن اضافه می‌شود.

نرم افزار آباکوس شامل پنج محصول اصلی می‌باشد که هرکدام برای کاربرد خاص خود مورد استفاده قرار می‌گیرند.

1. Abaqus/CAE (Complete Abaqus Environment): به طور کلی این محیط گرافیکی برای پیش پردازش و پس پردازش شبیه‌سازی مورد استفاده قرار می‌گیرد. با استفاده از محیط CAE می‌توان مدلسازی، تعریف خواص ماده و تعیین شرایط مرزی را انجام داد. همچنین با استفاده از ابزارهای قدرتمند این محیط می‌توان هندسه را مش‌بندی کرد و پس از آماده سازی مدل برای حلگر ، فرآیند حل را توسط آن نظارت کرد. در نهایت با استفاده از زیرمجموعه Viewer در این محیط، کاربر توانایی پردازش پس از حل و مشاهده نتایج شبیه سازی را دارد.

• Abaqus/ Standard: این محصول با هدف تحلیل و آنالیز انواع مسائل از جمله استاتیک، دینامیک، الکتریکی و … منتشر شده است. قابل ذکر است این محیط دستگاه معادلات را به صورت ضمنی در هر مرحله حل می‌کند و یکی از ابزارهای قدرتمند آباکوس برای حل معادلات و رسیدن به نتایج شبیه‌سازی می‌باشد. این حلگر توانایی انجام تحلیل‌های خطی و غیرخطی را دارد.

• Abaqus/Explicit: حلگر Explicit به طور خاص برای آنالیز مسائل غیر خطی گذرا و دینامیکی طراحی شده است. این محیط با استفاده از روش حل غیرضمنی توانایی شبیه سازی اینگونه مدل‌ها را با دقت بالا دارد. به طور مثال می‌توان مسائل ضربه، ، انفجار، فرمدهی و … را در این محیط تحلیل کرد. قابلیت حل با استفاده از انتگرال گیری صریح، این حلگر را قادر کرده است تا شبیه‌سازی مسائلی که محیط Standard توانایی و یا دقت کافی در آن را ندارد انجام دهد.

این ۵ محیط هسته‌های اصلی نرم‌افزار آباکوس می‌باشند و اکثر مسائل به کمک آن‌ها قابل تحلیل است. اگرچه زیرمجموعه‌های دیگری در هر یک از این محیط‌ها وجود دارد که به کمک آن می‌توان شبیه سازی‌های خاص را انجام داد. به عنوان مثال از محیط Aqua که زیرمجموعه دو بخش Standard و Explicit می‌باشد، برای شبیه سازی سازه‌های دریایی مانند سکوهای نفتی استفاده می‌شود.

نرم افزار انسیس‌ورکبنچ ANSYS WorkBench

نرم افزار انسیس ورک‌بنچ (Ansys Workbench) محصول شرکت انسیس (Ansys) می‌باشد که اولین نسخه تجاری آن در سال ۱۹۹۶ به صورت عمومی منتشر شد. انسیس که یکی از معروف ترین نرم‌افزارهای مهندسی در زمینه تحلیل المان محدود (Finite Element Analysis) است، توسط شرکت‌های زیادی در سراسر دنیا برای شبیه‌سازی به کار گرفته می‌شود.

نرم افزار کامسول COMSOL Multiphysics

نرم افزار مارک MSC Marc

نویسنده:
مهندس میلاد وحیدیان 
دانشجوی دکترای مهندسی مکانیک دانشگاه تهران

(برای مطالعه بیشتر روی نام یا تصویر ایشان کلیک کنید)