ارتعاشات آزاد و اجباری سیستم‌های گسسته (Free and Forced Vibrations of Discrete Systems)

مروری بر ارتعاشات آزاد و اجباری (Free and Forced Vibrations)

ارتعاشات آزاد (free vibrations) حالتی از حرکت نوسانی در یک سیستم مکانیکی است که پس از اعمال یک نیروی اولیه، سیستم بدون دریافت هیچ نیروی خارجی اضافی به نوسانات خود ادامه می‌دهد. این نوع ارتعاشات تنها تحت تأثیر نیروهای داخلی سیستم قرار دارند که معمولاً به دلیل خاصیت الاستیک (elastic property) یا بازگرداننده‌ای مانند یک فنر ایجاد می‌شوند. در چنین شرایطی، سیستم به طور مداوم با فرکانسی که به ویژگی‌های ذاتی آن بستگی دارد نوسان می‌کند. این فرکانس، به فرکانس طبیعی (natural frequency) سیستم معروف است و تنها به ویژگی‌های فیزیکی سیستم مانند جرم (mass)، سفتی (stiffness)، و میرایی (damping) وابسته است.

در یک سیستم مکانیکی، فرکانس طبیعی یکی از پارامترهای مهم است که تعیین می‌کند سیستم چگونه و با چه سرعتی نوسان می‌کند. به عنوان مثال، در یک سیستم فنر-جرم ساده، فرکانس طبیعی به میزان سفتی فنر (که نیروی بازگرداننده سیستم است) و جرم سیستم (که تمایل سیستم به مقاومت در برابر تغییرات سرعت است) وابسته است. افزایش جرم سیستم باعث کاهش فرکانس طبیعی و کاهش جرم باعث افزایش آن می‌شود. به همین ترتیب، افزایش سفتی سیستم منجر به افزایش فرکانس طبیعی و کاهش سفتی آن باعث کاهش فرکانس طبیعی می‌شود.

در حالت ایده‌آل، اگر هیچ نوع میرایی (damping) وجود نداشته باشد، سیستم می‌تواند برای همیشه به نوسانات خود ادامه دهد. میرایی به نیروهایی مانند اصطکاک (friction) یا مقاومت هوا اشاره دارد که در نهایت باعث کاهش انرژی نوسانی سیستم می‌شوند. این نیروها باعث می‌شوند که دامنه نوسانات به مرور زمان کاهش یابد و سیستم به تدریج به حالت تعادل برسد. در حالت نظری، یک سیستم بدون میرایی می‌تواند بی‌نهایت به نوسانات خود ادامه دهد، اما در دنیای واقعی، همیشه نیروهای میرایی وجود دارند که باعث متوقف شدن تدریجی نوسانات می‌شوند. این نیروهای میرایی انرژی جنبشی سیستم را جذب می‌کنند و آن را به گرما تبدیل می‌کنند، که نتیجه آن کاهش دامنه نوسانات است.

مثال‌های متداول از سیستم‌های دارای میرایی شامل حرکت یک پاندول (که به دلیل اصطکاک در محور آن و مقاومت هوا به تدریج متوقف می‌شود) یا نوسان یک سیم ویولن هستند. در هر دو حالت، با گذشت زمان، میرایی باعث از بین رفتن انرژی نوسانی شده و نوسانات متوقف می‌شوند. مقدار و نوع میرایی به نوع سیستم بستگی دارد؛ برخی سیستم‌ها با میرایی بالا به سرعت متوقف می‌شوند، در حالی که در سیستم‌هایی با میرایی کم، نوسانات مدت بیشتری ادامه خواهند داشت.

در مقابل، ارتعاشات اجباری (forced vibrations) زمانی رخ می‌دهد که یک سیستم مکانیکی تحت تأثیر نیرویی خارجی و متغیر در زمان قرار بگیرد. به عبارت دیگر، نیرویی از خارج به سیستم اعمال می‌شود و باعث می‌شود که سیستم با فرکانس نیروی اعمالی به نوسان درآید، نه با فرکانس طبیعی خود. به عنوان مثال، تصور کنید که یک سیستم جرم-فنر را به صورت متناوب با دست تکان دهید؛ سیستم با فرکانس حرکات دست شما به نوسان در می‌آید، حتی اگر این فرکانس با فرکانس طبیعی سیستم متفاوت باشد.

در این نوع ارتعاشات، یکی از مهم‌ترین مسائل که مهندسان باید به آن توجه کنند، پدیده‌ای به نام رزونانس (resonance) است. این پدیده زمانی رخ می‌دهد که فرکانس نیروی اعمالی خارجی با فرکانس طبیعی سیستم برابر می‌شود. در این شرایط، انرژی به طور مؤثر به سیستم منتقل می‌شود و دامنه نوسانات به طور چشمگیری افزایش می‌یابد. در حقیقت، در این حالت سیستم شروع به جذب مقدار زیادی انرژی می‌کند و این باعث افزایش شدید دامنه نوسانات می‌شود.

پدیده رزونانس (Resonance Phenomenon)

رزونانس (Resonance) یکی از مهم‌ترین و خطرناک‌ترین پدیده‌هایی است که در ارتعاشات اجباری رخ می‌دهد. این پدیده زمانی اتفاق می‌افتد که فرکانس نیروی خارجی اعمال‌شده با فرکانس طبیعی سیستم مطابقت داشته باشد. در این حالت، انرژی از نیروی خارجی به‌طور بسیار مؤثری به سیستم منتقل می‌شود و باعث افزایش قابل توجه دامنه نوسانات می‌شود. این افزایش دامنه می‌تواند به حدی برسد که سیستم نتواند نیروهای اعمال شده را تحمل کند و در نتیجه، خرابی جدی در سیستم به وجود آید.

به عنوان مثال، در سازه‌های بزرگ مانند پل‌ها یا ساختمان‌های بلند، اگر فرکانس نیرویی مانند باد یا زمین‌لرزه با فرکانس طبیعی سازه مطابقت داشته باشد، پدیده رزونانس رخ می‌دهد و دامنه ارتعاشات به شدت افزایش می‌یابد. یکی از معروف‌ترین نمونه‌های تاریخی این پدیده، فروپاشی پل تاکوما ناروز در سال 1940 است که به دلیل رزونانس ناشی از باد رخ داد. به همین دلیل، در طراحی سازه‌ها و ماشین‌آلات، مهندسان سعی می‌کنند از پدیده رزونانس جلوگیری کنند یا آن را کنترل کنند.

برای جلوگیری از بروز رزونانس، مهندسان از تکنیک‌های مختلفی استفاده می‌کنند. یکی از این تکنیک‌ها، اضافه کردن سیستم‌های میرای اضافی (مثل دمپرها) به سیستم است که انرژی اضافی را جذب کرده و از افزایش دامنه نوسانات جلوگیری می‌کنند. تکنیک دیگر، تغییر فرکانس طبیعی سیستم است؛ این کار می‌تواند از طریق تغییر جرم یا سفتی سیستم انجام شود تا فرکانس طبیعی سیستم از فرکانس نیروی خارجی فاصله بگیرد.

کاربردهای ارتعاشات آزاد در دنیای واقعی (Free Vibrations Applications)

ارتعاشات آزاد در بسیاری از سیستم‌های طبیعی و مهندسی دیده می‌شوند. هنگامی که سیستم‌ها تحت یک نیروی اولیه قرار گرفته و سپس بدون تأثیر نیروی خارجی نوسان می‌کنند، ارتعاشات آزاد رخ می‌دهد. در این بخش به چند نمونه از کاربردهای ارتعاشات آزاد در دنیای واقعی می‌پردازیم:

• پاندول در ساعت‌ها (Pendulum in Clocks): در ساعت‌های مکانیکی پاندولی، پاندول نقش بسیار مهمی در تنظیم زمان دارد. پس از جابجا شدن از موقعیت تعادل اولیه، پاندول به صورت آزادانه و با فرکانس طبیعی خود شروع به نوسان می‌کند. این فرکانس طبیعی عمدتاً به طول پاندول و شتاب جاذبه محلی وابسته است. هرچه طول پاندول بلندتر باشد، فرکانس نوسانات کمتر خواهد بود. به دلیل این ویژگی پایدار، پاندول‌های ساعت می‌توانند زمان را به دقت تنظیم کنند. دامنه نوسانات به مرور زمان به دلیل مقاومت هوا و اصطکاک در مفاصل کاهش می‌یابد، اما مکانیزم‌هایی مانند چرخ‌دنده‌ها و فنرها به پاندول کمک می‌کنند تا به نوسانات خود ادامه دهد.
• پاسخ سازه‌ها به زلزله (Response of Structures to Earthquakes): وقتی یک سازه مانند ساختمان یا پل در معرض نیروی زلزله قرار می‌گیرد، پس از پایان نیروی اولیه، سازه دچار ارتعاشات آزاد می شود. در حین زلزله سازه تحت ارتعاشات اجباری قرار دارد اما به محض اتمام زلزه سازه در معرض ارتعاش آزاد قرار می گیرد. این نوسانات با فرکانس طبیعی سازه رخ می‌دهند که به ویژگی‌های خاص سازه مانند جرم و سفتی آن بستگی دارد. به‌طور کلی، سازه‌هایی که برای مقابله با زلزله طراحی شده‌اند، باید بتوانند به خوبی با این نوسانات طبیعی مقابله کنند. میرایی داخلی سازه باعث کاهش تدریجی دامنه نوسانات می‌شود و سازه به آرامی به حالت تعادل بازمی‌گردد. بدون میرایی مناسب، نوسانات ممکن است بسیار زیاد شده و منجر به خرابی سازه در حین ارتعاشات اجباری (در حین زلزله) یا حین ارتعاشات آزاد (بعد از زلزله) شوند. بنابراین، تحلیل ارتعاشات آزاد و اجباری سازه‌ها برای طراحی سازه‌های مقاوم در برابر زلزله بسیار مهم است.
• سیم‌های موسیقی و سازهای زهی (Musical Strings): سیم‌های سازهای زهی مانند ویولن، گیتار، و پیانو نیز نمونه‌هایی از سیستم‌های ارتعاش آزاد هستند. پس از ضربه زدن به سیم یا کشیدن آرشه روی آن، سیم به‌صورت آزادانه و با فرکانس طبیعی خود نوسان می‌کند و صدایی با فرکانس مشخص تولید می‌کند. فرکانس نوسانات سیم به ویژگی‌هایی مانند طول، ضخامت و تنش سیم بستگی دارد. صدای تولید شده توسط این سیم‌ها، حاصل نوسانات آزاد آنهاست که پس از ضربه یا کشش اولیه، به مرور زمان کم می‌شود و در نهایت متوقف می‌شود. سیستم‌های میرایی طبیعی مانند مقاومت هوا و اصطکاک در نقطه اتصال، این نوسانات را کاهش می‌دهند.
• تیرهای سازه‌ای و سیستم‌های معلق (Structural Beams and Suspended Systems): بسیاری از سیستم‌های سازه‌ای، مانند تیرهای فولادی یا پل‌های معلق، پس از وارد شدن نیرویی ناگهانی مانند برخورد وسایل نقلیه یا زلزله، دچار ارتعاشات آزاد می‌شوند. این ارتعاشات می‌توانند بسته به فرکانس طبیعی سازه و خواص مصالح استفاده شده، به صورت نوسانات طولانی‌مدت یا کوتاه‌مدت مشاهده شوند. تحلیل ارتعاشات آزاد در چنین سیستم‌هایی برای ارزیابی پایداری سازه‌ها و جلوگیری از شکست‌های مکانیکی بسیار مهم است.

کاربردهای ارتعاشات اجباری در دنیای واقعی (Forced Vibrations Applications)

ارتعاشات اجباری زمانی رخ می‌دهند که یک سیستم تحت تأثیر نیرویی خارجی قرار گیرد که به‌طور پیوسته به آن اعمال می‌شود. این نوع ارتعاشات در بسیاری از کاربردهای مهندسی و صنعتی مهم هستند. در ادامه، به برخی از نمونه‌های ارتعاشات اجباری در دنیای واقعی اشاره می‌کنیم:

• ماشین‌آلات دوار (Rotating Machinery): در ماشین‌آلات دوار مانند توربین‌ها، کمپرسورها و پمپ‌ها، ارتعاشات اجباری به دلیل نیروهای خارجی پیوسته مانند عدم تعادل جرم‌ها، تغییرات فشار و نیروی موتور رخ می‌دهد. این نیروهای خارجی باعث می‌شوند که سیستم با فرکانس نیروی اعمالی نوسان کند، که می‌تواند مشکلاتی مانند افزایش سایش و خرابی زودهنگام قطعات را به دنبال داشته باشد. اگر فرکانس نیروی اعمالی با فرکانس طبیعی سیستم مطابقت داشته باشد، ممکن است پدیده رزونانس رخ دهد و دامنه ارتعاشات به شدت افزایش یابد که منجر به خرابی‌های مکانیکی جدی شود. بنابراین، طراحی دقیق و استفاده از دمپرها و سیستم‌های بالانسینگ در چنین ماشین‌آلاتی ضروری است.
• ساختمان‌ها تحت تأثیر بارهای بادی (Buildings under Wind Loads): ساختمان‌های بلند مانند برج‌ها و آسمان‌خراش‌ها به‌طور مداوم تحت تأثیر نیروهای بادی قرار دارند. این نیروهای باد ممکن است به صورت متناوب به سازه وارد شوند و باعث ایجاد ارتعاشات اجباری در آن شوند. اگر فرکانس این نیروها با فرکانس طبیعی ساختمان مطابقت داشته باشد، پدیده رزونانس رخ داده و دامنه ارتعاشات می‌تواند به حدی برسد که ساختمان به‌طور خطرناکی نوسان کند. برای جلوگیری از چنین پدیده‌ای، در طراحی‌های مدرن از سیستم‌های میرای جرم تنظیم‌شده (Tuned Mass Dampers) استفاده می‌شود. این سیستم‌ها انرژی اضافی ارتعاشات را جذب کرده و از افزایش دامنه نوسانات جلوگیری می‌کنند.
• ارتعاشات موتور خودرو (Car Engine Vibrations): در موتورهای احتراق داخلی، هر چرخه احتراق نیرویی به پیستون‌ها و اجزای دیگر موتور وارد می‌کند که باعث ایجاد ارتعاشات اجباری می‌شود. این ارتعاشات به دلیل ماهیت دوره‌ای فرآیند احتراق به‌طور مداوم در موتور رخ می‌دهند. اگر این ارتعاشات به خوبی کنترل نشوند، می‌توانند منجر به سایش زودهنگام قطعات، افزایش مصرف سوخت و کاهش کارایی موتور شوند. به همین دلیل، طراحی موتورهای خودرو شامل سیستم‌های کنترل ارتعاشات مانند بالانسینگ دقیق قطعات متحرک و استفاده از پایه‌های موتور ضد ارتعاش است.
• ماشین‌های لباسشویی و خشک‌کن‌ها (Washing Machines and Dryers): ماشین‌های لباسشویی و خشک‌کن‌ها نیز نمونه‌هایی از سیستم‌های دچار ارتعاشات اجباری هستند. هنگامی که درام این ماشین‌ها با سرعت زیاد چرخش می‌کند، نیروهای نامتعادل ناشی از لباس‌ها باعث ایجاد ارتعاشات اجباری در ماشین می‌شود. طراحی‌های مدرن شامل سیستم‌های بالانسینگ و استفاده از میرایی برای کاهش لرزش و جلوگیری از حرکت اضافی ماشین‌ها است.
• خطوط انتقال نیرو (Power Transmission Lines): خطوط انتقال نیرو نیز به‌طور مداوم تحت تأثیر نیروهای بادی قرار می‌گیرند که می‌تواند باعث ارتعاشات اجباری در سیم‌های برق شود. این نوسانات در طول زمان می‌تواند باعث خستگی فلز سیم و در نهایت پاره شدن آن‌ها شود. برای جلوگیری از این پدیده، از دمپرهای ویژه‌ای در خطوط انتقال استفاده می‌شود تا این نوسانات کاهش یابند.

ارتعاش آزاد در سیستم‌های مکانیکی (Free Vibration in Mechanical Systems)

ارتعاش آزاد زمانی رخ می‌دهد که سیستم پس از اعمال یک نیروی اولیه بدون تأثیر نیروهای خارجی نوسان کند. به عبارت دیگر، هنگامی که یک سیستم به دلیل یک تغییر یا اختلال اولیه از حالت تعادل خود خارج می‌شود و سپس بدون دریافت نیروی خارجی دیگر به نوسانات خود ادامه می‌دهد، این ارتعاشات به عنوان “ارتعاشات آزاد” شناخته می‌شوند. برای مثال، اگر یک آونگ را از حالت سکون به یک زاویه کوچک حرکت دهیم و سپس رها کنیم، آونگ بدون تأثیر نیروی خارجی نوسان می‌کند. این نوسانات تنها تحت تأثیر نیروهای داخلی سیستم مانند نیروی گرانش و اینرسی جرم هستند.

نیروی بازگرداننده در این سیستم‌ها معمولاً به دلیل خاصیت الاستیکی (مانند نیروی یک فنر) یا نیروی گرانشی است که به سیستم اعمال می‌شود. ویژگی کلیدی ارتعاشات آزاد این است که فرکانس و رفتار نوسانی سیستم تنها به ویژگی‌های ذاتی آن مانند جرم، سفتی، و انرژی اولیه‌ای که به سیستم داده شده است، بستگی دارد.

معادله حرکت ارتعاشات آزاد بدون میرا کننده (Free Motion Equation Without Damping)

برای تحلیل این نوع نوسانات در یک سیستم مکانیکی ساده، معادله حرکت سیستم جرم-فنر به‌عنوان یک مدل پایه برای بررسی ارتعاشات آزاد بدون میرایی استفاده می‌شود. این معادله بر اساس قانون دوم نیوتن و با توجه به نیروهای بازگرداننده و اینرسی جرم نوشته می‌شود. معادله حرکت در یک سیستم جرم-فنر ساده به صورت زیر است:

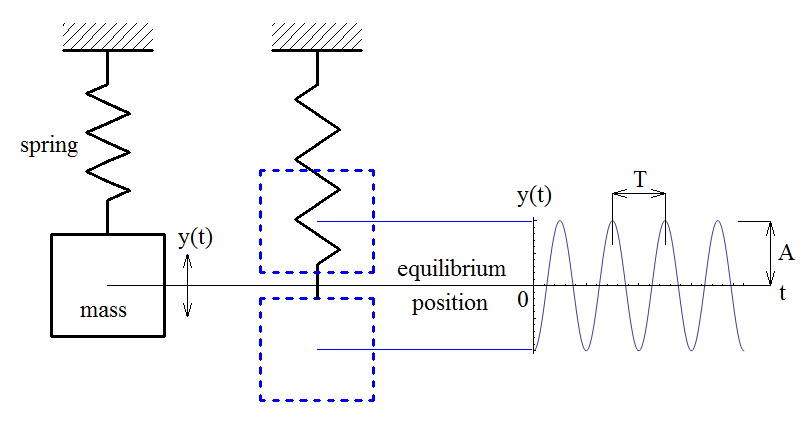
در این معادله:

• m: جرم سیستم است. جرم سیستم در حقیقت معیاری از مقدار ماده‌ای است که باید نوسان کند. افزایش جرم سیستم باعث کاهش سرعت نوسان می‌شود، زیرا جرم بیشتر به انرژی بیشتری برای تغییر سرعت نیاز دارد.
• k: سفتی فنر است. سفتی فنر نشان‌دهنده میزان نیروی بازگرداننده‌ای است که سیستم در ازای تغییر مکان تجربه می‌کند. هرچه سفتی فنر بیشتر باشد، سیستم با نیروی بیشتری به سمت حالت تعادل بازمی‌گردد و در نتیجه فرکانس نوسان نیز افزایش می‌یابد.
• x: جابجایی سیستم از موقعیت تعادل است. جابجایی، موقعیت لحظه‌ای سیستم نسبت به نقطه تعادل را نشان می‌دهد.
• x¨: شتاب سیستم است. شتاب سیستم نشان‌دهنده سرعت تغییرات سرعت حرکت سیستم است و از طریق این متغیر می‌توان رفتار نوسانی سیستم را توصیف کرد.

این معادله بیان می‌کند که نیروی بازگرداننده فنر (kx) به اندازه کافی قوی است تا جرم را به سمت حالت تعادل برگرداند، بدون اینکه نیروهای خارجی در سیستم وجود داشته باشد. معادله‌ای که حاصل می‌شود یک معادله دیفرانسیل هارمونیک ساده است که فرکانس طبیعی سیستم را تعیین می‌کند.

فرکانس طبیعی سیستم به صورت زیر تعریف می‌شود:

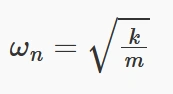
این فرمول بیان می‌کند که فرکانس طبیعی سیستم به میزان سفتی فنر و جرم سیستم وابسته است. سیستم‌هایی با جرم بیشتر یا سفتی کمتر، فرکانس نوسان کمتری خواهند داشت. به‌عبارت دیگر، سیستم سنگین‌تر یا ضعیف‌تر کندتر نوسان خواهد کرد.

پاسخ عمومی سیستم برای جابجایی بر حسب زمان به صورت زیر بیان می‌شود:

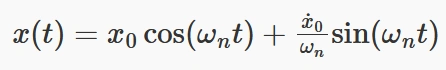
این معادله نشان می‌دهد که جابجایی سیستم در هر لحظه، تابعی از شرایط اولیه آن (مقدار جابجایی اولیه x0 و سرعت اولیه x˙0) و همچنین فرکانس طبیعی سیستم ωn است. در واقع، جابجایی سیستم از حالت تعادل، ترکیبی از دو مؤلفه سینوسی و کسینوسی است که به صورت همزمان باهم ترکیب می‌شوند و نوسان سیستم را تشکیل می‌دهند.

همچنین، حرکت هارمونیک سیستم را می‌توان به شکل دیگری نیز بیان کرد:

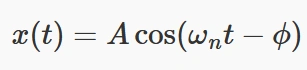
که در آن:

در این معادله، A بیانگر دامنه نوسانات است و نشان‌دهنده بزرگ‌ترین میزان انحراف سیستم از حالت تعادل است. مقدار دامنه به شرایط اولیه سیستم بستگی دارد؛ هرچه انرژی بیشتری در ابتدای نوسان به سیستم داده شود، دامنه نوسانات نیز بیشتر خواهد بود.

زاویه فاز ϕ نشان‌دهنده میزان تأخیر زمانی است و به صورت زیر تعریف می‌شود:

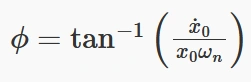
زاویه فاز مشخص می‌کند که حرکت سیستم از کدام نقطه در چرخه نوسان شروع می‌شود. به عبارت دیگر، تعیین می‌کند که سیستم در لحظه آغاز نوسانات در چه وضعیتی قرار دارد. این مقدار بستگی به جابجایی و سرعت اولیه سیستم در زمان شروع نوسانات دارد.

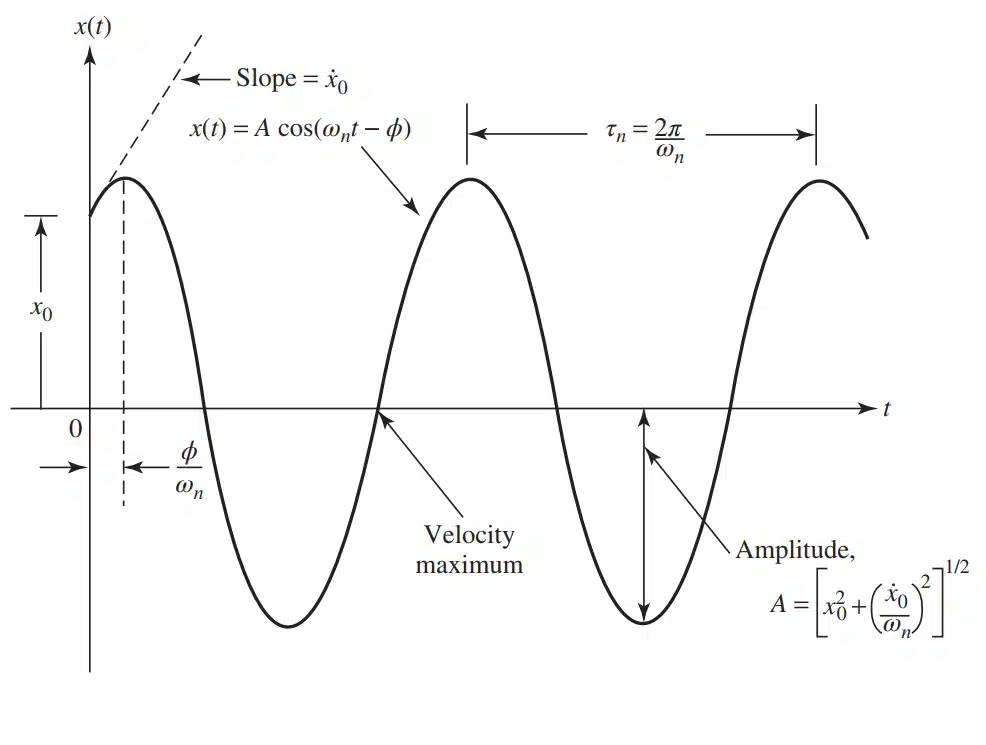
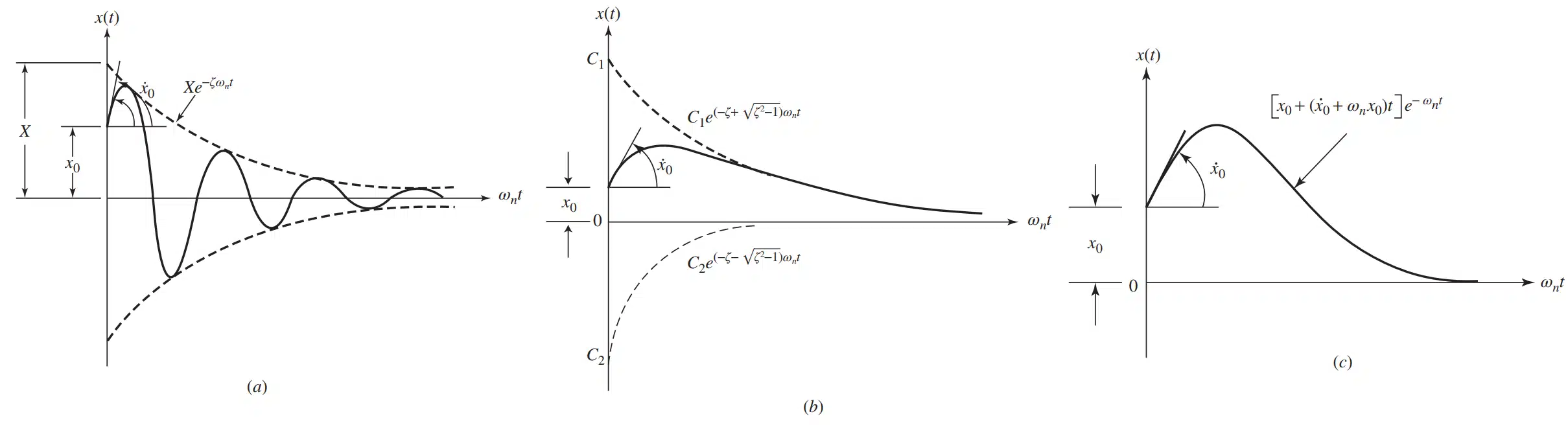
نوسانات سیستم به صورت سینوسی بوده و دوره تناوب آن τn=2π/ωn است. این نمودار نشان می‌دهد که سیستم‌های مکانیکی پس از اعمال یک نیروی اولیه، تا زمانی که نیروی میرا کننده‌ای وجود نداشته باشد، به نوسان ادامه می‌دهند. به این معنا که در غیاب هر گونه نیرویی که باعث از بین رفتن انرژی نوسانات شود (مانند اصطکاک یا میرایی)، سیستم به صورت نامحدود به نوسانات خود ادامه می‌دهد.

با این حال، در دنیای واقعی نیروهای میرایی مانند اصطکاک یا مقاومت هوا وجود دارند که باعث می‌شوند دامنه نوسانات به مرور زمان کاهش یابد و سیستم به حالت تعادل بازگردد. در نتیجه، سیستم‌های واقعی به مرور زمان انرژی خود را از دست داده و نوسانات آن‌ها به تدریج متوقف می‌شوند.

معادله حرکت ارتعاشات آزاد به همراه میرا کننده (Free Motion Equation With Damping)

در حالت ارتعاشات آزاد با میرایی، معادله حرکت را با تقسیم تمامی پارامتر ها به جرم سیستم می توان به شکل زیر در آورد:

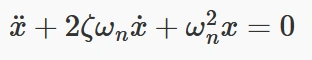
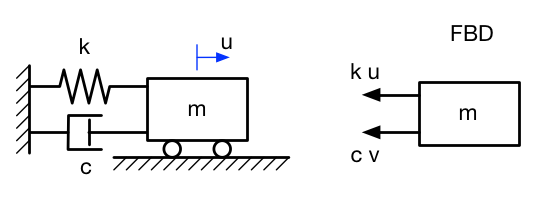
نسبت میرایی ζ بر اساس ضریب میرایی c به صورت زیر تعریف می‌شود:

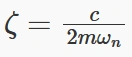
سیستم بسته به مقدار ζ می‌تواند در یکی از سه حالت زیر قرار بگیرد:

1. زیر بحرانی (Underdamped, ζ<1): این حالت زمانی رخ می‌دهد که میزان میرایی سیستم کمتر از حد بحرانی باشد. در این شرایط، سیستم همچنان به نوسان ادامه می‌دهد، اما دامنه نوسانات به تدریج کاهش می‌یابد. اگرچه انرژی نوسانات از دست می‌رود، اما این کاهش به اندازه‌ای سریع نیست که نوسانات متوقف شوند. این حالت به ویژه در بسیاری از سیستم‌های مکانیکی، از جمله خودروها و سازه‌های مهندسی دیده می‌شود که در آن‌ها سیستم نیاز دارد تا به سرعت به حالت تعادل بازگردد اما نه به صورت فوری و ناگهانی. در این حالت، نوسانات به مرور زمان کم می‌شوند اما سیستم کاملاً به سکون نمی‌رسد. در نتیجه سیستم می‌تواند برای مدت زیادی به نوسان ادامه دهد، اما با دامنه کاهشی.
2. فوق بحرانی (Overdamped, ζ>1): در حالت فوق بحرانی، سیستم به قدری میرا شده است که به آرامی و بدون هیچ نوسانی به حالت تعادل بازمی‌گردد. این حالت معمولاً برای سیستم‌هایی مطلوب است که سرعت بازگشت به تعادل اهمیت چندانی ندارد اما نوسانات به هیچ وجه نباید رخ دهند. به عنوان مثال، در برخی از سیستم‌های هیدرولیکی یا مکانیکی که نیاز به حرکت آرام و کنترل شده دارند، استفاده از میرایی فوق بحرانی ضروری است. در این حالت، سیستم بدون نوسان، اما به‌طور تدریجی به حالت تعادل برمی‌گردد.
3. بحرانی (Critical Damping, ζ=1): این حالت زمانی رخ می‌دهد که میزان میرایی سیستم برابر با مقدار بحرانی باشد. در این حالت، سیستم به سرعت به حالت تعادل بازمی‌گردد بدون اینکه هیچ نوسانی رخ دهد. این حالت ایده‌آل برای سیستم‌هایی است که می‌خواهند بدون نوسان به سرعت به حالت تعادل بازگردند. برای مثال، در سیستم‌های تعلیق خودروها، میرایی بحرانی می‌تواند تضمین کند که پس از عبور از یک دست‌انداز، خودرو به سرعت و بدون نوسانات اضافی به حالت تعادل بازمی‌گردد. اگر میرایی بیشتر از این حد باشد، سیستم می‌تواند کندتر به حالت تعادل برسد و اگر کمتر باشد، سیستم دچار نوسانات ناخواسته خواهد شد.

حالت 1: دمپ زیر بحرانی (ζ<1)

در این حالت، سیستم همچنان نوسان می‌کند، اما دامنه نوسانات با گذشت زمان کاهش می‌یابد. این کاهش دامنه به دلیل از دست دادن انرژی در هر چرخه نوسان است که عمدتاً به واسطه میرایی در سیستم رخ می‌دهد. این نوع میرایی در بسیاری از سیستم‌های مکانیکی دیده می‌شود که در آن‌ها نوسانات مورد نظر است، اما نیاز به کاهش تدریجی آن وجود دارد.

پاسخ ارتعاشی در حالت زیر بحرانی به صورت زیر است:

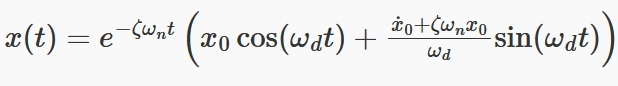
این معادله بیان می‌کند که دامنه نوسانات با ضریب ζ و ωn (فرکانس طبیعی سیستم) به‌طور نمایی کاهش می‌یابد. به عبارت دیگر، در هر چرخه از نوسان، بخشی از انرژی به دلیل میرایی از سیستم خارج می‌شود و باعث می‌شود که نوسانات به تدریج کاهش یابد و به حالت تعادل برسد. فرکانس نوسانات در حالت زیر بحرانی برابر با ωd=ωn1−ζ2 است که نشان می‌دهد نوسانات سیستم با فرکانسی کمتر از فرکانس طبیعی رخ می‌دهد.

حالت 2: دمپ فوق بحرانی (ζ>1)

در حالت دمپ فوق بحرانی، سیستم به آرامی و بدون هیچ نوسانی به تعادل بازمی‌گردد. در این حالت، میرایی به حدی زیاد است که سیستم به تدریج و بسیار آهسته به حالت تعادل بازمی‌گردد. این حالت زمانی مفید است که نوسانات سیستم نباید به هیچ وجه رخ دهند، هرچند که ممکن است سیستم مدت بیشتری برای رسیدن به تعادل نیاز داشته باشد.

پاسخ در این حالت به صورت زیر است:

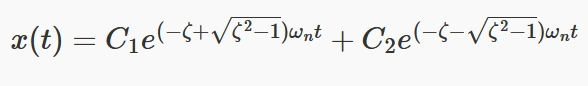
این معادله نشان‌دهنده دو عبارت نمایی است که یکی از آن‌ها حرکت سریع‌تری به سمت تعادل دارد و دیگری حرکت کندتری دارد. ترکیب این دو عامل باعث می‌شود که سیستم به صورت کنترل‌شده و بدون نوسان به تعادل برسد. در این حالت، سرعت بازگشت به تعادل کمتر از حالت بحرانی است اما بدون نوسان رخ می‌دهد.

حالت 3: دمپ بحرانی (ζ=1)

دمپ بحرانی حالتی است که در آن میرایی به اندازه‌ای است که سیستم به سرعت و بدون هیچ نوسانی به حالت تعادل بازمی‌گردد. در این حالت، سیستم دقیقاً در نقطه‌ای قرار دارد که میرایی باعث جلوگیری از نوسان شده اما بازگشت به تعادل به حداکثر سرعت خود می‌رسد. این نوع میرایی در بسیاری از سیستم‌های مکانیکی و مهندسی مورد استفاده قرار می‌گیرد که نیاز به بازگشت سریع به حالت تعادل دارند.

معادله حرکت در حالت دمپ بحرانی به شکل زیر است:

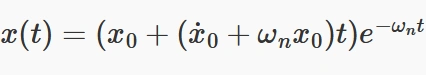
در اینجا، پاسخ سیستم نشان می‌دهد که سیستم هیچ نوسانی نمی‌کند و به سرعت به سمت نقطه تعادل خود حرکت می‌کند. تمامی حرکت به سمت تعادل بدون هیچ‌گونه تغییر در جهت رخ می‌دهد و سیستم به سرعت پایدار می‌شود.

ارتعاشات اجباری تحت نیروی هارمونیک (Forced Vibrations with Harmonic Force)

ارتعاشات اجباری زمانی رخ می‌دهند که یک نیروی خارجی متناوب یا هارمونیک به یک سیستم مکانیکی اعمال شود. در این حالت، سیستم مکانیکی مجبور می‌شود تا با فرکانس نیروی اعمالی نوسان کند. یکی از ساده‌ترین حالت‌ها، زمانی است که سیستم بدون میرایی باشد و تحت نیروی هارمونیک به شکل f(t)=f0cos⁡(ωt) قرار گیرد. این نیرو به‌طور مستمر و با فرکانس ω به سیستم وارد می‌شود.

در چنین سیستمی، معادله حرکت به صورت زیر نوشته می‌شود:

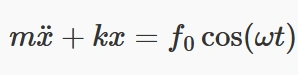
این معادله نشان‌دهنده این است که نیروهای بازگرداننده و اینرسی در سیستم جرم-فنر باید با نیروی خارجی وارد شده به سیستم مقابله کنند. نیروی بازگرداننده توسط فنر با سفتی k و اینرسی سیستم با جرم m نمایان می‌شوند. نیروی هارمونیک f0cos⁡(ωt) عامل نوسانات اجباری است و به سیستم تحمیل می‌شود.

پاسخ حالت پایدار (Steady-State Response)

پاسخ حالت پایدار معادله، که نشان‌دهنده رفتار طولانی‌مدت سیستم پس از گذشت حالت گذرای سیستم است، به شکل زیر بیان می‌شود:

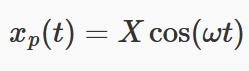
که در آن:

• X دامنه نوسانات حالت پایدار است،
• ω فرکانس نیروی اعمالی است،
• f0 بزرگی نیروی هارمونیک است.

دامنه نوسانات حالت پایدار به شکل زیر محاسبه می‌شود:

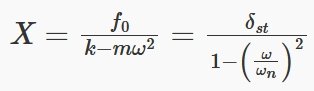
در اینجا:

δst انحراف استاتیکی جرم تحت اثر نیروی f0 است که به عنوان نسبت نیروی استاتیک به سفتی فنر تعریف می‌شود:

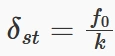
ωn فرکانس طبیعی سیستم است و بیانگر فرکانس ذاتی نوسانات آزاد سیستم می‌باشد:

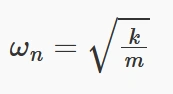
این فرمول نشان‌دهنده رابطه‌ای بین دامنه نوسانات و نسبت فرکانس نیروی اعمالی به فرکانس طبیعی سیستم است. اگر ω به ωn نزدیک شود، دامنه نوسانات به طرز قابل توجهی افزایش می‌یابد، که این به پدیده رزونانس مرتبط است.

رزونانس (Resonance)

رزونانس زمانی رخ می‌دهد که فرکانس نیروی اعمالی با فرکانس طبیعی سیستم برابر شود. در این حالت، سیستم در بالاترین دامنه نوسان خود قرار می‌گیرد و اگر نیروی میرایی وجود نداشته باشد، دامنه به طور مداوم افزایش می‌یابد. این حالت می‌تواند به آسیب‌های جدی در سیستم منجر شود. در حالت رزونانس، نسبت فرکانس نیروی اعمالی به فرکانس طبیعی برابر با 1 است:

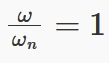
در حالت رزونانس، پاسخ ارتعاشات اجباری (Forced Vibration) به شکل زیر است:

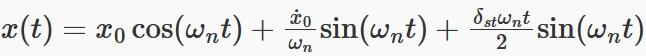
این معادله نشان می‌دهد که دامنه نوسانات با گذشت زمان به‌طور نامحدود افزایش می‌یابد. این افزایش مداوم دامنه ناشی از هم‌راستایی فرکانس نیروی اعمالی با فرکانس طبیعی سیستم است و می‌تواند باعث ناپایداری و خرابی سیستم شود. در واقع، رزونانس یکی از دلایل اصلی خرابی مکانیکی در سیستم‌هایی است که تحت تأثیر نیروهای هارمونیک قرار می‌گیرند.

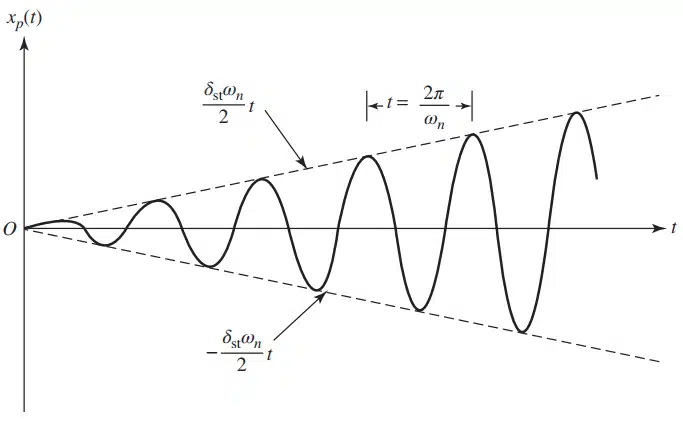
در بسیاری از کاربردهای مهندسی، پدیده رزونانس یک تهدید جدی برای سیستم‌های مکانیکی است. به همین دلیل، در طراحی ماشین‌آلات و سازه‌ها، باید از وقوع رزونانس جلوگیری شود. یکی از راهکارهای رایج برای مقابله با رزونانس استفاده از دمپرها و سیستم‌های میرایی است که انرژی نوسانات را جذب کرده و از افزایش دامنه نوسانات جلوگیری می‌کنند. همچنین، تنظیم جرم و سفتی سیستم‌ها می‌تواند باعث تغییر فرکانس طبیعی آن‌ها شود و سیستم را از حالت رزونانس دور کند.

سیستم میرایی‌دار تحت نیروی هارمونیک (Damped System Under Harmonic Force)

وقتی یک سیستم دارای میرایی ویسکوز تحت نیروی هارمونیک f(t)=f0cos⁡(ωt) قرار می‌گیرد، معادله حرکت به صورت زیر است:

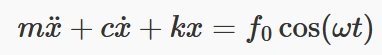
پاسخ خصوصی معادله به شکل زیر بیان می‌شود:

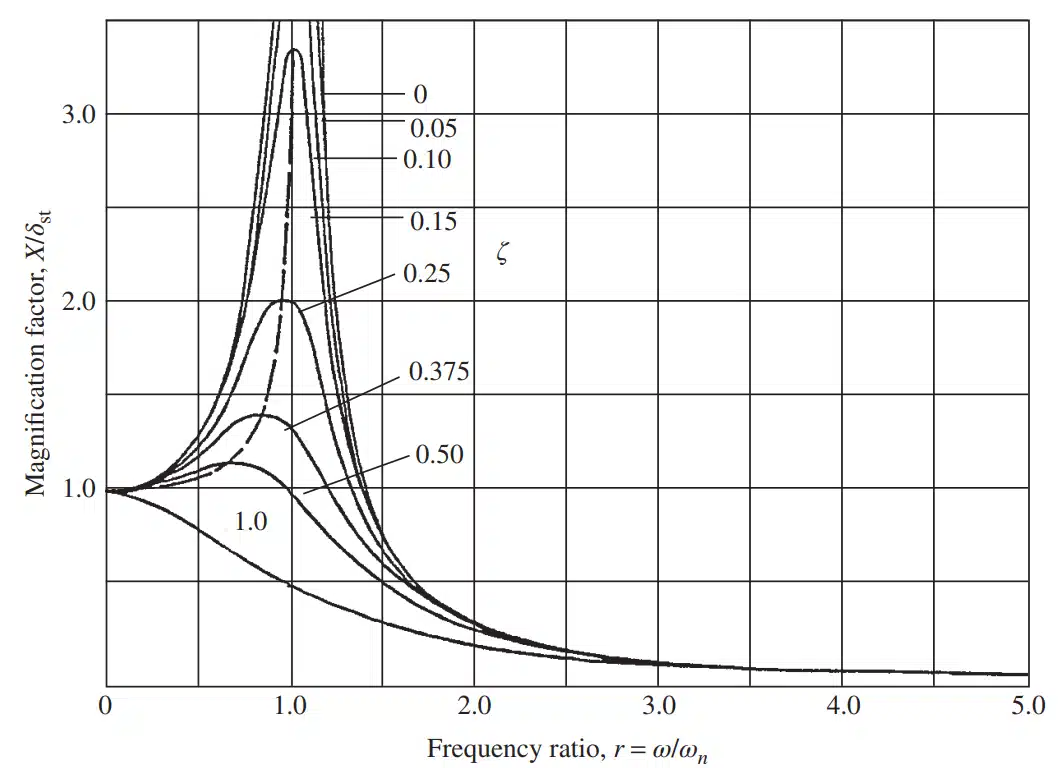
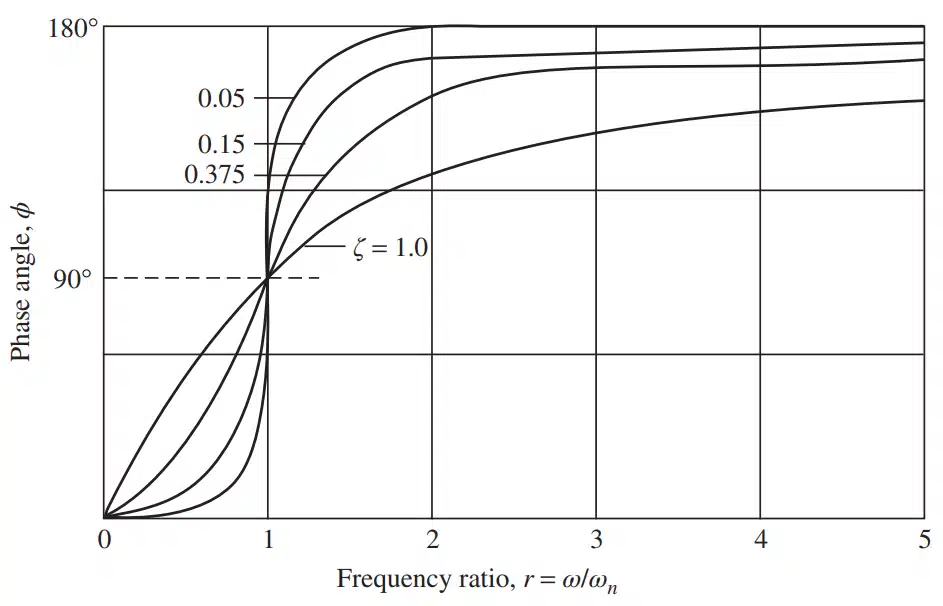
ارتعاش سیستم‌های چند درجه آزادی (Multi-degree-of-Freedom Systems)

سیستم‌های چند درجه آزادی (MDOF) به عنوان مدلی برای تحلیل و بررسی رفتار ارتعاشی سیستم‌هایی با بیش از یک درجه آزادی استفاده می‌شوند. به عبارت دیگر، هر درجه آزادی نشان‌دهنده یک متغیر مستقل برای توصیف حرکت سیستم است. در بسیاری از سیستم‌های مهندسی مانند سازه‌ها، ماشین‌آلات، و سازه‌های مکانیکی پیچیده، چندین درجه آزادی وجود دارد که باید برای تحلیل رفتار دینامیکی سیستم در نظر گرفته شوند.

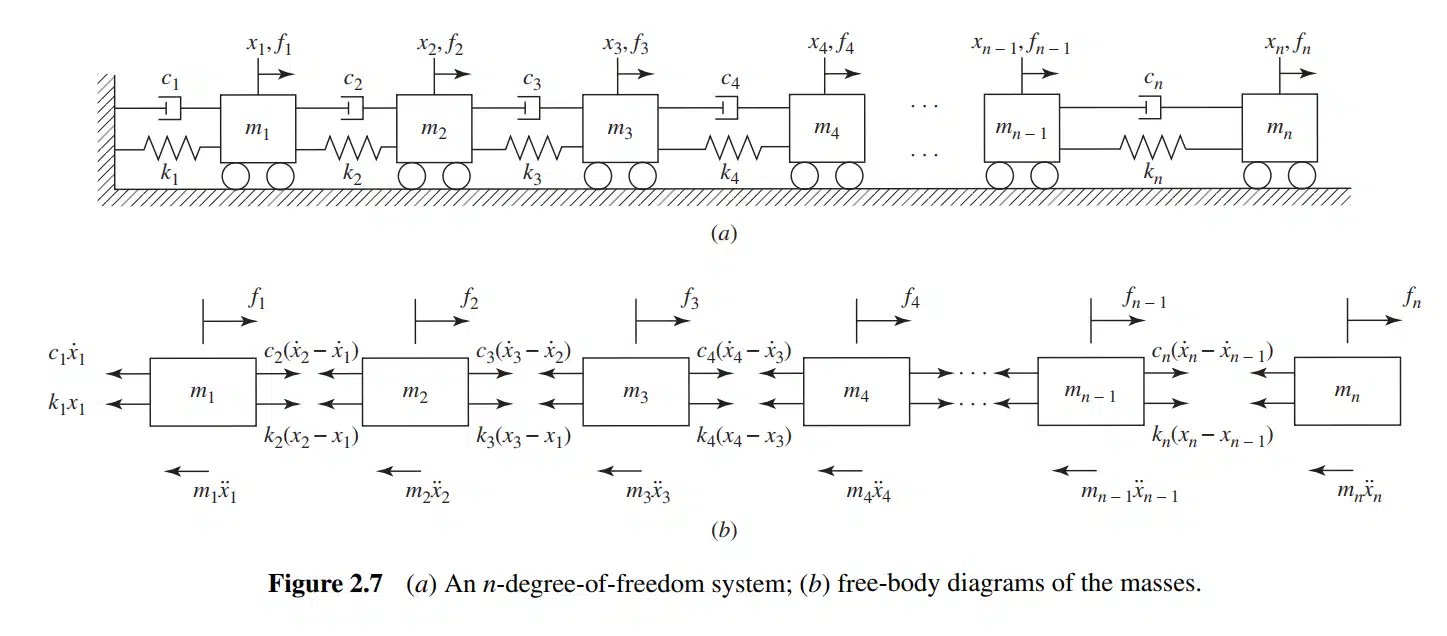
مدل‌های MDOF معمولاً با استفاده از معادلات حرکت کوپل‌شده که توصیف‌کننده جابجایی‌ها، سرعت‌ها، و شتاب‌های جرم‌های مختلف هستند، بیان می‌شوند. با استفاده از این معادلات می‌توان ارتعاشات سیستم را به دقت تحلیل و پاسخ آن را در برابر نیروهای خارجی یا ورودی‌های اولیه بررسی کرد. شکل زیر یک نمونه از سیستم MDOF را نشان می‌دهد که شامل چندین جرم، فنر، و دمپر است.

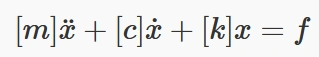
در این معادله، [m] ماتریس جرم، [c] ماتریس میرایی، و [k] ماتریس سفتی سیستم را نشان می‌دهند. این ماتریس‌ها وابسته به ویژگی‌های فیزیکی سیستم هستند و نحوه تعامل اجزای مختلف سیستم با یکدیگر را توصیف می‌کنند. بردار x جابجایی‌های جرم‌های مختلف، بردار x˙ سرعت‌ها، و بردار x¨ شتاب‌های سیستم را شامل می‌شود. همچنین بردار f نشان‌دهنده نیروهای خارجی وارد شده به جرم‌های سیستم است.

به عنوان مثال، در یک سازه چندطبقه، هر طبقه می‌تواند به عنوان یک جرم در نظر گرفته شود که تحت تأثیر نیروهای افقی مانند زلزله یا باد قرار می‌گیرد. فنرها نشان‌دهنده سفتی اتصالات بین طبقات هستند و دمپرها نیز میزان میرایی انرژی ارتعاشی را نشان می‌دهند. این مدل‌ها در تحلیل دینامیک سازه‌ها و ماشین‌آلات پیچیده بسیار کاربرد دارند.

ماتریس‌های جرم، میرایی و سفتی (Mass, Damping, and Stiffness Matrices)

ماتریس‌های جرم، میرایی، و سفتی سیستم‌های MDOF به شکل زیر تعریف می‌شوند. این ماتریس‌ها به ما امکان می‌دهند تا به صورت کوپل‌شده تمامی جابجایی‌ها، سرعت‌ها، و شتاب‌ها را به‌طور همزمان در سیستم بررسی کنیم.

این معادلات نشان می‌دهند که رفتار دینامیکی هر جرم وابسته به تعامل آن با جرم‌های همسایه است. به عنوان مثال، سفتی سیستم و نحوه اتصال جرم‌ها از طریق فنرها در معادله‌های ماتریسی سفتی نمایان می‌شوند. میرایی سیستم نیز به طور مشابه توزیع میرایی بین اجزا را نشان می‌دهد.

بردارهای جابجایی، سرعت و شتاب (Displacement, Velocity, and Acceleration Vectors)

بردارهای x، x˙، و x¨ به ترتیب جابجایی‌ها، سرعت‌ها، و شتاب‌های جرم‌های مختلف سیستم را نشان می‌دهند. همچنین، بردار f نیروهای وارد شده به جرم‌های سیستم را شامل می‌شود.

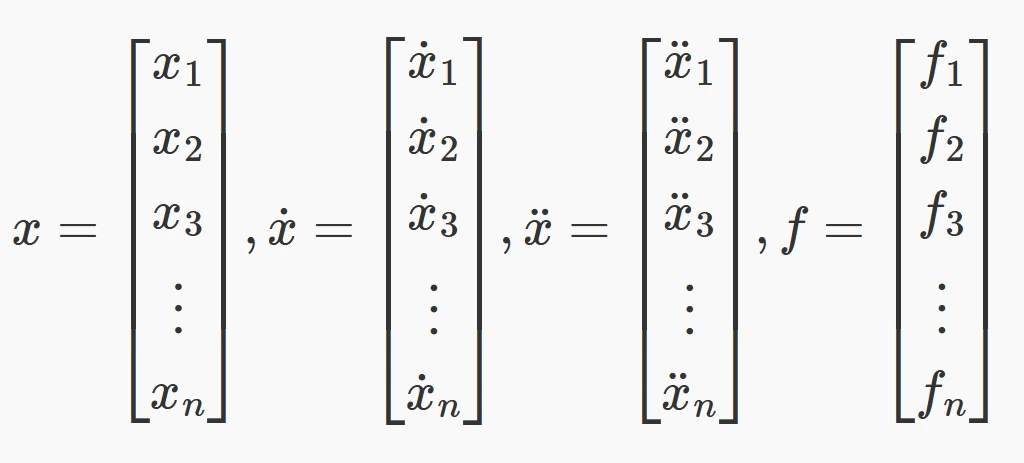
این بردارها برای حل معادلات حرکت در سیستم‌های چند درجه آزادی استفاده می‌شوند. با ترکیب این بردارها با ماتریس‌های جرم، میرایی، و سفتی، می‌توان پاسخ سیستم به تحریکات خارجی را محاسبه کرد. به‌عنوان مثال، در یک سازه زلزله‌ای، نیروهای وارد شده از زلزله در بردار f نمایش داده می‌شوند و با حل معادلات، جابجایی‌های طبقات سازه محاسبه می‌شود.

مدل‌سازی سیستم‌های پیوسته به عنوان سیستم‌های چند درجه آزادی (Modeling Continuous Systems as MDOF Systems)

بسیاری از سیستم‌های فیزیکی به صورت پیوسته هستند، به‌عنوان مثال تیرها، کابل‌ها، یا لوله‌های بلند. در این سیستم‌ها، جابجایی‌ها و رفتار دینامیکی در نقاط مختلف توزیع شده‌اند و به صورت پیوسته تغییر می‌کنند. با این حال، برای تحلیل راحت‌تر و کاربردی‌تر، می‌توان این سیستم‌های پیوسته را به صورت سیستم‌های چند درجه آزادی (MDOF) مدل‌سازی کرد. این کار از طریق روش‌هایی مانند روش المان محدود (Finite Element Method, FEM) یا روش گسسته‌سازی نقاط انجام می‌شود.

در روش گسسته‌سازی، یک سیستم پیوسته به مجموعه‌ای از جرم‌ها، فنرها، و دمپرها تقسیم می‌شود. هر جرم نمایانگر بخشی از سیستم پیوسته است و فنرها نشان‌دهنده سفتی یا تغییر شکل سیستم هستند. به این ترتیب، یک سیستم پیوسته می‌تواند به عنوان یک سیستم MDOF مدل‌سازی شود که هر جرم نماینده یک نقطه از سیستم پیوسته است.

برای مثال، یک تیر پیوسته می‌تواند به تعداد زیادی المان‌های جرم-فنر گسسته تقسیم شود که هر المان یک بخش کوچک از تیر را نشان می‌دهد. با افزایش تعداد المان‌ها، دقت مدل‌سازی بهبود می‌یابد و می‌توان رفتار سیستم پیوسته را با دقت بالاتری شبیه‌سازی کرد.

این روش‌ها به ما این امکان را می‌دهند که سیستم‌های پیچیده و پیوسته را به سادگی و با استفاده از مدل‌های گسسته تحلیل کرده و پاسخ دینامیکی آن‌ها را در برابر نیروهای خارجی یا ورودی‌های دیگر بررسی کنیم.

مزایای استفاده از مدل MDOF در تحلیل دینامیکی (Advantages of MDOF in Dynamic Analysis)

استفاده از مدل‌های MDOF در تحلیل دینامیکی سیستم‌ها چندین مزیت دارد:

• امکان تحلیل دقیق‌تر سیستم‌های پیچیده با چندین درجه آزادی.
• امکان در نظر گرفتن تأثیرات متقابل بین اجزای سیستم.
• قابلیت استفاده از روش‌های عددی مانند تحلیل مودال و روش المان محدود برای حل معادلات حرکت.
• مدل‌سازی سیستم‌های پیوسته به عنوان سیستم‌های چند درجه آزادی و تحلیل ساده‌تر.

نتیجه‌گیری (Conclusion)

ارتعاشات آزاد و اجباری در سیستم‌های مکانیکی، به عنوان دو پدیده اساسی، تحلیل رفتار دینامیکی این سیستم‌ها را ممکن می‌سازند. در ارتعاشات آزاد، سیستم به دلیل ویژگی‌های ذاتی خود، مانند جرم، سفتی و میرایی، بدون نیاز به نیروی خارجی نوسان می‌کند. این نوع ارتعاشات به ویژه در سیستم‌هایی مانند سازه‌های ساختمانی، سازهای موسیقی و بسیاری از ماشین‌آلات قابل مشاهده است. در این حالت، فرکانس طبیعی سیستم نقش کلیدی ایفا می‌کند و سیستم به صورت هارمونیک در حالتی پایدار نوسان می‌کند، مگر آنکه میرایی موجود باعث کاهش تدریجی دامنه شود.

در مقابل، ارتعاشات اجباری زمانی رخ می‌دهند که یک نیروی خارجی به طور مداوم به سیستم اعمال می‌شود. این نیرو می‌تواند از منابع مختلفی مانند نیروهای بادی، نیروهای لرزه‌ای یا نیروهای ناشی از ماشین‌آلات دوار نشأت بگیرد. در این حالت، فرکانس نیروی اعمالی تعیین‌کننده رفتار نوسانی سیستم است. پدیده رزونانس زمانی به وجود می‌آید که فرکانس نیروی خارجی با فرکانس طبیعی سیستم هم‌پوشانی داشته باشد، که می‌تواند منجر به افزایش چشمگیر دامنه نوسانات شود و در نهایت سیستم مکانیکی را در معرض آسیب‌های جدی قرار دهد. مدیریت و کنترل این نوع ارتعاشات با استفاده از تکنیک‌های مختلفی مانند دمپرها و تنظیم فرکانس طبیعی سیستم انجام می‌گیرد.

مدل‌های چند درجه آزادی (MDOF) به ما این امکان را می‌دهند که رفتار دینامیکی سیستم‌های پیچیده‌تر، از جمله سازه‌های بزرگ و سیستم‌های پیوسته مانند تیرها و کابل‌ها را به دقت تحلیل کنیم. این مدل‌ها با استفاده از ماتریس‌های جرم، میرایی و سفتی، سیستم‌های چند جرمی را شبیه‌سازی می‌کنند و به ما اجازه می‌دهند تا تاثیر نیروهای خارجی و ارتعاشات داخلی را به طور همزمان در نظر بگیریم. همچنین، تبدیل سیستم‌های پیوسته به مدل‌های گسسته (MDOF) از طریق روش‌هایی مانند روش المان محدود (FEM) امکان‌پذیر است، که دقت بالاتری در تحلیل سیستم‌های واقعی ارائه می‌دهد.

در نهایت، درک کامل ارتعاشات آزاد و اجباری و توانایی تحلیل دقیق این پدیده‌ها برای مهندسان بسیار حیاتی است. این دانش نه تنها به پیشگیری از خرابی‌های مکانیکی کمک می‌کند، بلکه به بهبود عملکرد، بهره‌وری و ایمنی سیستم‌های مهندسی نیز می‌انجامد. استفاده از مدل‌های دقیق مانند سیستم‌های چند درجه آزادی، به ما این امکان را می‌دهد که به چالش‌های پیچیده‌ای مانند رزونانس و ارتعاشات اجباری با دقت و کارایی بیشتری پاسخ دهیم.